If the plates of a parallel plate capacitor are not equal in area then quantity of charge
On the plates will be same but nature of charge will differ
On the plates as will as nature of charge will be different
On the plates will be different but nature of charge will be same
As well as nature of charge will be same
To solve the question regarding the quantity of charge in a parallel plate capacitor with unequal plate areas, we can follow these steps:
1. Understanding the Capacitor Configuration:
- We have a parallel plate capacitor with two plates that are not equal in area. Let's denote the area of the positive plate as A1 and the area of the negative plate as A2.
2. Charge Distribution:
- When a charge Q is supplied to the capacitor, it will distribute itself across the plates. The positive plate will have a charge of +Q and the negative plate will have a charge of −Q.
3. Effective Area:
- The effective area of the capacitor is determined by the smaller of the two plate areas because the electric field is only produced in the overlapping region. Therefore, the effective area Aeff can be defined as:
Aeff=min(A1,A2)
4. Electric Field Calculation:
- The electric field E between the plates can be calculated using the formula:
E=σε0
where σ is the surface charge density given by σ=QAeff and ε0 is the permittivity of free space.
5. Capacitance Calculation:
- The capacitance C of the capacitor can be calculated using the formula:
C=QV
where V is the potential difference across the plates. The potential difference can be expressed in terms of the electric field and the separation d between the plates:
V=E⋅d
Hence, substituting for E:
C=Q(QAeffε0)d=Aeffε0d
6. Conclusion:
- The charge Q on the plates remains the same in magnitude but is distributed according to the effective area of the capacitor. The nature of the charge is opposite on the two plates, with one plate being positively charged and the other negatively charged.
Final Answer:
The quantity of charge Q on the capacitor plates remains equal in magnitude but is influenced by the effective area of the capacitor, which is determined by the smaller of the two plate areas.
- We have a parallel plate capacitor with two plates that are not equal in area. Let's denote the area of the positive plate as A1 and the area of the negative plate as A2.
- When a charge Q is supplied to the capacitor, it will distribute itself across the plates. The positive plate will have a charge of +Q and the negative plate will have a charge of −Q.
- The effective area of the capacitor is determined by the smaller of the two plate areas because the electric field is only produced in the overlapping region. Therefore, the effective area Aeff can be defined as:
Aeff=min(A1,A2)
- The electric field E between the plates can be calculated using the formula:
E=σε0
where σ is the surface charge density given by σ=QAeff and ε0 is the permittivity of free space.
- The capacitance C of the capacitor can be calculated using the formula:
C=QV
where V is the potential difference across the plates. The potential difference can be expressed in terms of the electric field and the separation d between the plates:
V=E⋅d
Hence, substituting for E:
C=Q(QAeffε0)d=Aeffε0d
- The charge Q on the plates remains the same in magnitude but is distributed according to the effective area of the capacitor. The nature of the charge is opposite on the two plates, with one plate being positively charged and the other negatively charged.
The quantity of charge Q on the capacitor plates remains equal in magnitude but is influenced by the effective area of the capacitor, which is determined by the smaller of the two plate areas.
Similar Questions
In figure , the plates of a parallel plate capacitors have unequal charges. Its capacitance is C. P is a point outside the capacitor and close to the plate of charge -Q. The distance between the plates is d. Then

View SolutionIn the figure shown the plates of a parallel plate capacitor have unequal charges. Its capacitance is 'C' P is a point outside the capacitor and close to the plate of charge −Q. The distance between the plates is 'd'

View Solution
Knowledge Check
The plates of a parallel plate capacitor are, not exactly parallel. The surface charge density therefore :
Ahigher at the closer endBthe surface charge density will not be uniformCeach plate will have the same potential at each point.Dthe electric field is smallest where the plates are closest.The plates of a parallel plate capacitor are, not exactly parallel. The surface charge density therefore :
AIs higher at the closer endBThe surface charge densitywill not be uniformCEach plate will have the same potential at each pointDThe electric field is smallest where the plates are closestIf we pull apart the plates of parallel plate capacitor then,
AThe capacitance increasesBTotal charge increasesCThe potential difference increasesDCapacitance increases
A.P.D. of V volts is applied across the plates of a parallel plate capacitor having plate area A. if Q is the charge on its plates and K is the dielectric constant of the medium, between the plates, then the plate separation is given by
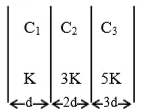
View SolutionIn the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
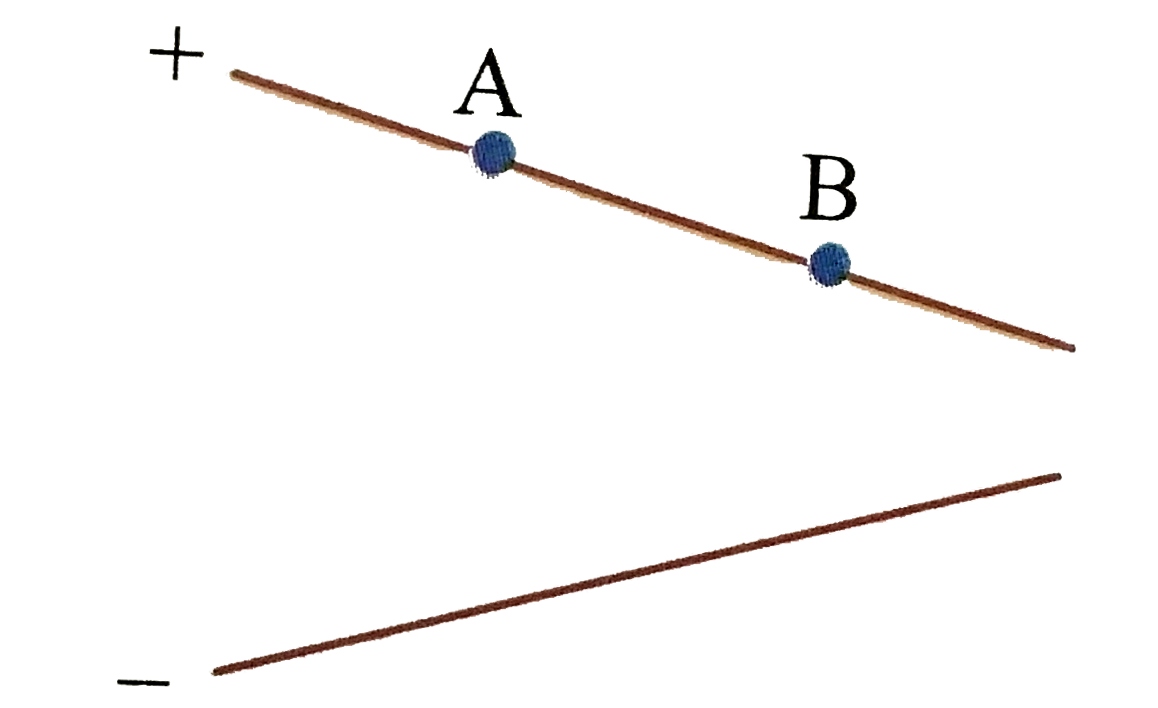
View SolutionThe plates of a parallel plate capacitor are charged by a battery and the battery is disconnected after the charging. Now, the plates are placed as shown in the figure. Then (plates are not parallel to each other).
 .
.
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)

View SolutionThe plates of a parallel plate capacitor are charged with a battery so that the plates of the capacitor have acquired the P.D. equal to e.m.f of the battery. The ratio of the work done by the battery and the energy stored in capacitor is
View Solution
