The distance between the plates of a parallel plate capacitor is 3 mm the potential difference applied is 3×105 V. If an electron travels from one plate to another the change in its potential energy is
3×105 eV
900 eV
108 eV
Negligible
To find the change in potential energy of an electron traveling between the plates of a parallel plate capacitor, we can follow these steps:
Step 1: Identify the given values
- Distance between the plates, d=3mm=3×10−3m
- Potential difference, ΔV=3×105V
- Charge of an electron, e=1.6×10−19C
Step 2: Write the formula for change in potential energy
The change in potential energy (ΔU) when a charge (q) moves through a potential difference (ΔV) is given by:
ΔU=q⋅ΔV
Step 3: Substitute the values into the formula
Here, the charge q is the charge of an electron, which is −e (the negative sign indicates that the electron has a negative charge). However, since we are interested in the magnitude of the change in potential energy, we can use the absolute value:
ΔU=e⋅ΔV
Substituting the values:
ΔU=(1.6×10−19C)⋅(3×105V)
Step 4: Calculate the change in potential energy
Now, perform the multiplication:
ΔU=1.6×3×10−19×105
ΔU=4.8×10−14J
Step 5: Convert to electron volts (optional)
Since 1eV=1.6×10−19J, we can convert the energy into electron volts:
ΔU=4.8×10−14J1.6×10−19J/eV=3×105eV
Final Answer
The change in potential energy of the electron is:
ΔU=4.8×10−14Jor3×105eV
---
- Distance between the plates, d=3mm=3×10−3m
- Potential difference, ΔV=3×105V
- Charge of an electron, e=1.6×10−19C
The change in potential energy (ΔU) when a charge (q) moves through a potential difference (ΔV) is given by:
ΔU=q⋅ΔV
Here, the charge q is the charge of an electron, which is −e (the negative sign indicates that the electron has a negative charge). However, since we are interested in the magnitude of the change in potential energy, we can use the absolute value:
ΔU=e⋅ΔV
Substituting the values:
ΔU=(1.6×10−19C)⋅(3×105V)
Now, perform the multiplication:
ΔU=1.6×3×10−19×105
ΔU=4.8×10−14J
Since 1eV=1.6×10−19J, we can convert the energy into electron volts:
ΔU=4.8×10−14J1.6×10−19J/eV=3×105eV
The change in potential energy of the electron is:
ΔU=4.8×10−14Jor3×105eV
Similar Questions
The distance between the plates of a parallel plate capacitor is "4cm" .An electric field of 2×104V/m is established between the plates.It is then disconnected from the battery and an uncharged metal plate of thickness "1cm" is inserted into the capacitor parallel to it's plates.The potential difference between the plates of capacitor after the introduction of the metal plate is k×102V .The value of ' "k" s
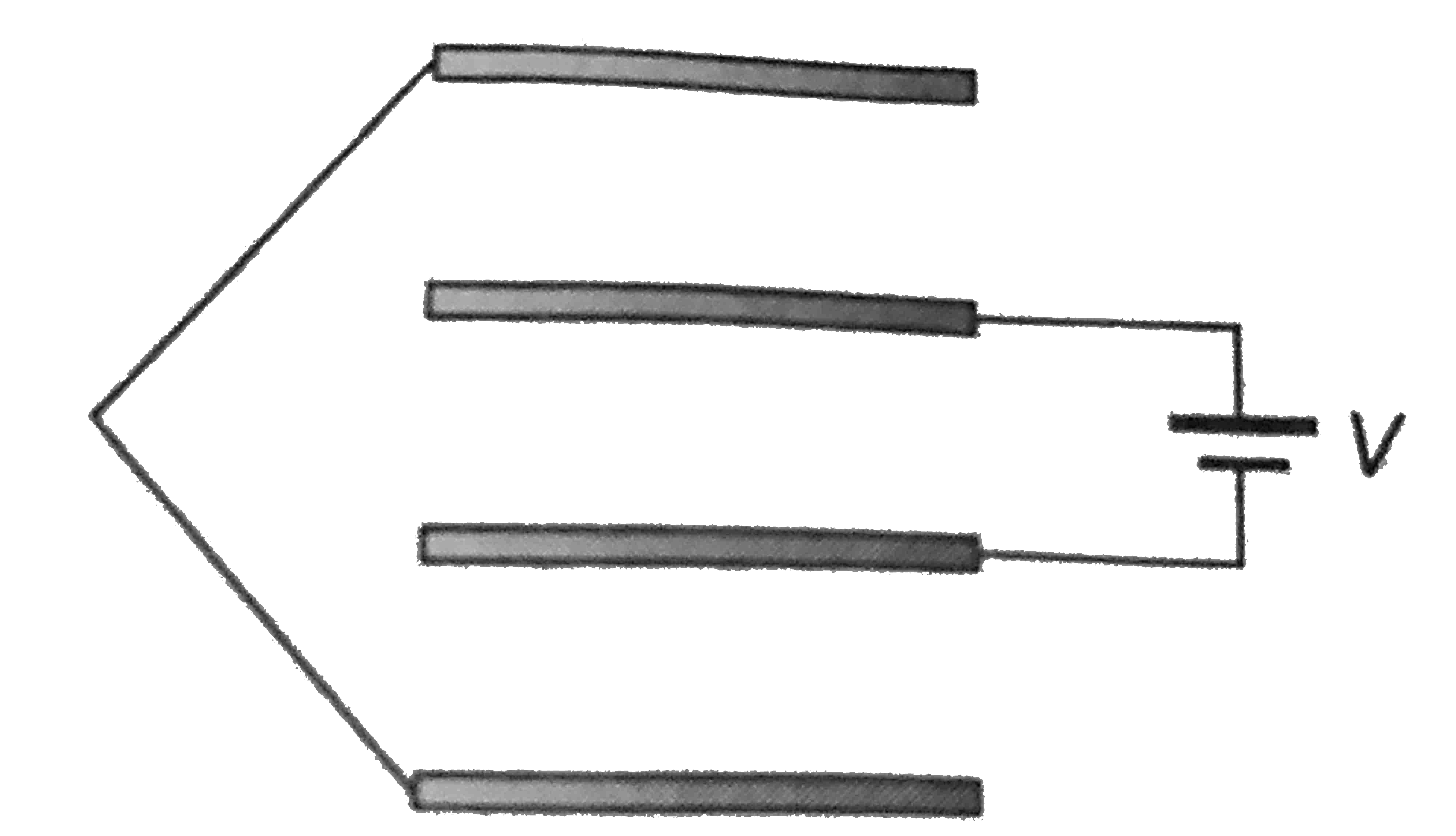
View Solution(a) Find the potential difference between the plates of a parallel plate capacitor of capacitance 5μF if a charge +800μC is placed on one plate and-200μC on another plate.
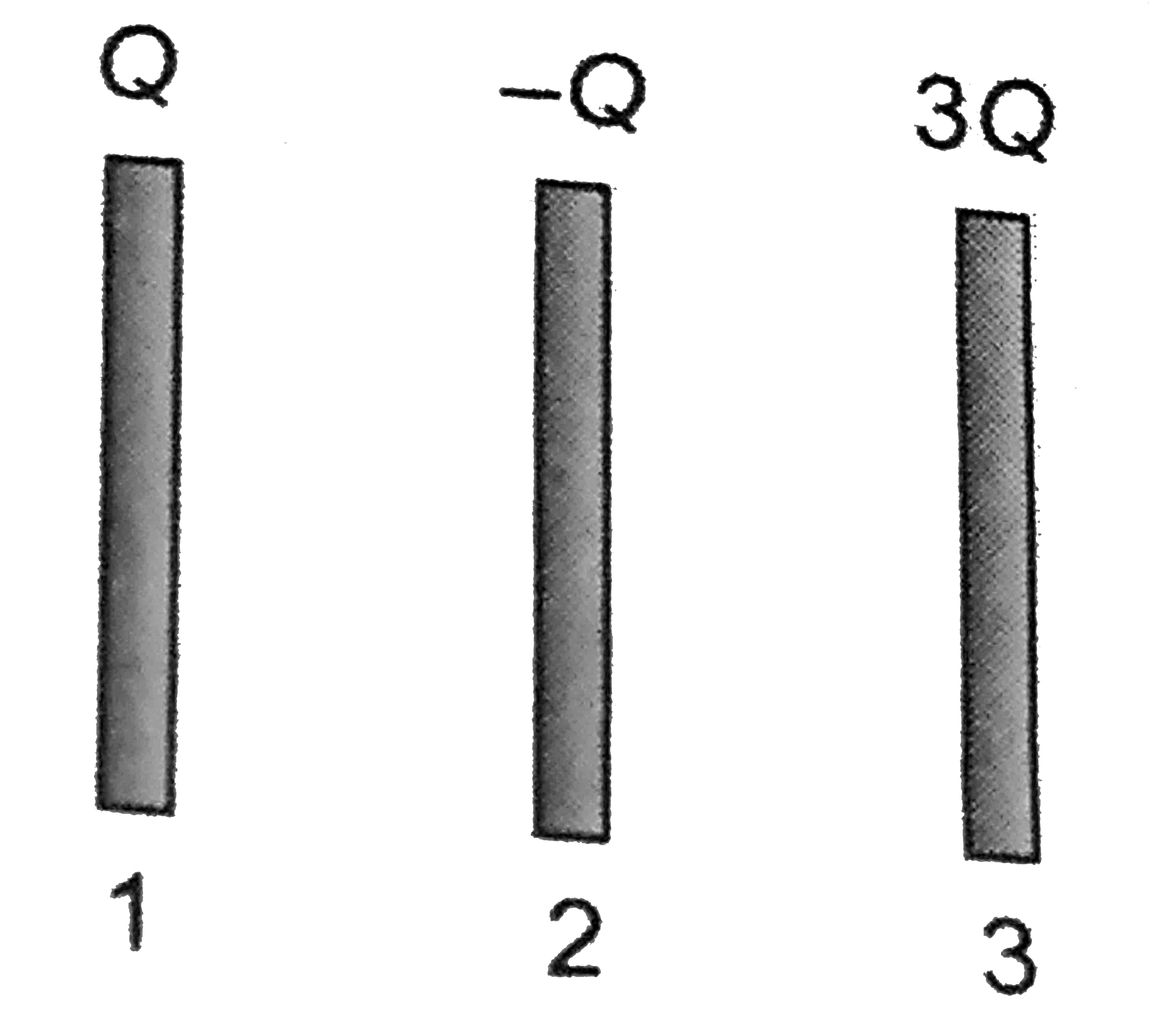
(b) The charege given to plate are as shown. The capacitance between the adjacent plates is C. find the charge on outer surface of plate 3, and potential difference between plate 1 and 2.
(c) If A is area of each plate and d is separation between adjacent plates, find the charge supplied by battery.
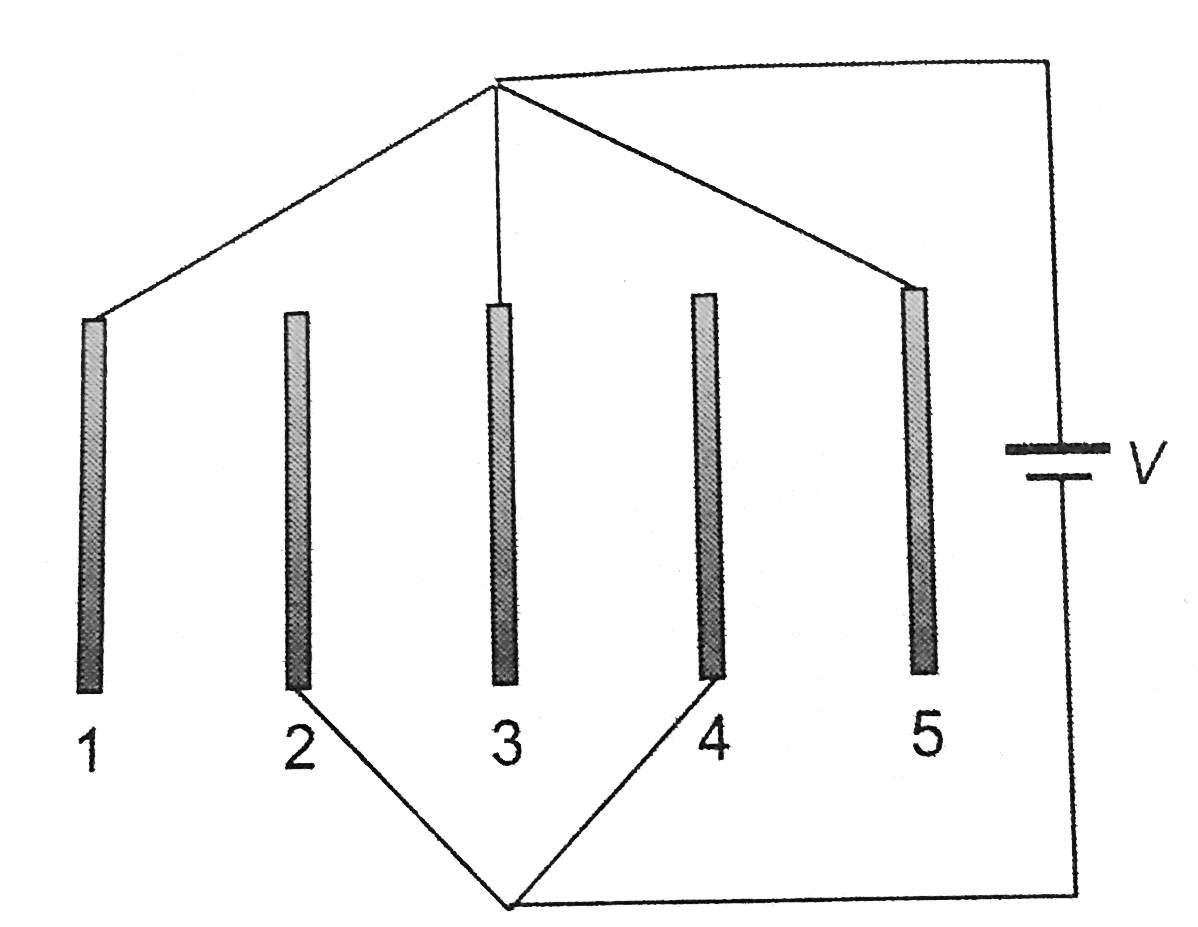
(d) Five idential capacitor plates each of area A are arranged such that adjacent plates are at a distance d apart. the plates are connected to a source of emf V as shown. what is the magnitude and nature of charge on plates 1 and 3 respectively?
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
Achances of electrical break down will increases if potential difference between the plates is kept constant.Bchance of electrical break down will decreases if potential difference between the plates is kept constant.Cchance of electric break down will increases if charge on the plates is kept constantDchance of electrical break down will decrease if charge on the plate is kept constant.The distance between the plates of a parallel plate condenser is 4mm and potential difference is 60 volts. If the distance between the plates is increased to 12mm, then
AThe potential difference of the condenser will become 180 voltsBThe potential difference will become 20 voltsCThe potential difference will remain unchangedDThe charge on condenser will reduce to one thirdWhat is the area of the plates of a 3 F parallel plate capacitor, if the sepreration between the plates is 5 mm ?
A1.694×109m2B4.529×109m2C9.281×109m2D12.981×109m2
In a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
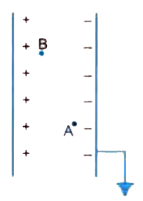
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionIn Millikan's oil drop experiment an oil drop of radius r and change Q is held in equilibrium between the plates of a charged parallel plate capacitor when the potential change is V. To keep a drop radius 2r and with a change 2Q is equilibriu between the plates the potential difference V' required is:
View SolutionThe potential difference between the plates of a parallel plate capacitor is 10V and separation is 5 cm. Find the energy density between plates. (ε0=10−11F/m)
View Solution