Question

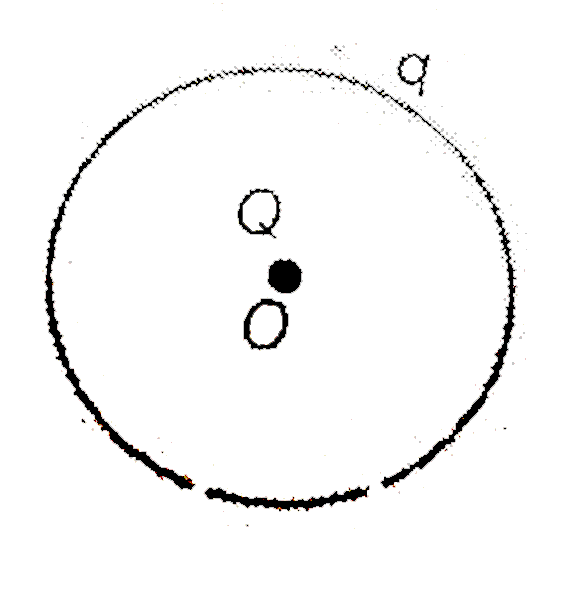
A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R $>$ r). The potential difference between the two is

Options

A. proportional to Q
B. Proportional to q
C. Dependent on both Q and q
D. independent of both Q and q

Answer

B

Explanation

To find the potential difference between a spherical conductor of charge $$q$$ and radius $$r$$ placed at the center of a spherical shell of radius $$R$$ and charge $$Q$$ (where $$R>r$$), we can follow these steps:

1. Understanding the System:
- We have a spherical conductor (let's call it SC) with charge \( q \) and radius \( r \).
- This conductor is placed at the center of a spherical shell (let's call it SS) with charge \( Q \) and radius \( R \).

2. Potential Inside the Spherical Conductor:
- The potential \( V_{SC} \) at the surface of the spherical conductor is given by the formula:
\( V_{SC} = \frac{kq}{r} \)
- Here, \( k \) is the electrostatic constant.

3. Potential Outside the Spherical Shell:
- For the spherical shell, since it is a conductor, the potential outside the shell (at a distance greater than \( R \)) is given by:
\( V_{SS} = \frac{kQ}{R} \)

4. Potential Inside the Spherical Shell:
- Inside the shell (between the inner conductor and the shell), the potential is constant and equal to the potential at the surface of the shell:
\( V_{inside} = \frac{kQ}{R} \)

5. Calculating the Potential Difference:
- The potential difference \( \Delta V \) between the spherical conductor and the spherical shell is given by:
\( \Delta V = V_{SC} - V_{SS} \)
- Substituting the values we found:
\( \Delta V = \frac{kq}{r} - \frac{kQ}{R} \)

6. Final Expression:
- Therefore, the potential difference between the two is:
\( \Delta V = \frac{kq}{r} - \frac{kQ}{R} \)

Final Answer:
The potential difference between the spherical conductor and the spherical shell is:
\( \Delta V = \frac{kq}{r} - \frac{kQ}{R} \)