$I_{n}$ is the area of n sided refular polygon inscribed in a circle unit radius and $O_{n}$ be the area of the polygon circumscribing the given circle, prove that $I_{n} = \frac{O_{n}}{2} (1 + \sqrt{1 - {(\frac{2 I_{n}}{n})}^{2}})$

Video Solution

Text Solution

Verified by Experts

Let OAB be one triangle out of n of a n-sided polygon inscribed in a circle of radius 1. Then,
$∠ A O B = \frac{2 π}{n}$
$O A = O B = 1$

$∴ Area (Δ A O B) = \frac{1}{2} 1 \times 1 \times \sin (\frac{2 π}{n})$
$= \frac{1}{2} \sin (\frac{2 π}{n})$
Area of n -sided polygon $= I_{n} = \frac{n}{2} \sin . \frac{2 π}{n}$ ....(i)
Similarly, let O'A'B' be one of the triangle out of n of n-sided polygon escribing the circle of unit radius.
Then, in $D e t l a O' B' A', \cos . \frac{π}{n} = \frac{1}{O' B'}$
or $O' B' = \sec . \frac{π}{n}$
Area $(Δ O' B' A') = \frac{1}{2} {(O' B')}^{2} \sin (\frac{2 π}{n})$
$= \frac{1}{2} \sec^{2} (\frac{π}{n}) \sin (\frac{2 π}{n})$
Therefore, the area of n-sided polygon is given by
$(O_{n}) = \frac{n}{2} \sec^{2} . \frac{π}{n} \sin . \frac{2 π}{n}$ (ii)
From Eqs. (i) and (ii), we get
$\frac{I_{n}}{O_{n}} = \frac{\frac{n}{2} \sin . \frac{2 π}{n}}{\frac{n}{2} \sec^{2} . \frac{π}{n} \sin . \frac{2 π}{n}} = \frac{1}{\sec^{2} . \frac{π}{n}}$
or $I_{n} = (\cos^{2} . \frac{π}{n}) O_{n}$
$= \frac{O_{n}}{2} [1 + \cos (\frac{2 π}{n})]$
$= \frac{O_{n}}{2} [1 + \sqrt{1 - \sin^{2} . \frac{2 π}{n}}]$
$= \frac{O_{n}}{2} [1 - \sqrt{1 - {(\frac{2 I_{n}}{n})}^{2}}]$

Updated on:21/07/2023

If r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
A $\frac{a}{2} cot (\frac{π}{2 n})$
B $\frac{a}{2} cot (\frac{π}{n})$
C $\frac{a}{2} tan (\frac{π}{n})$
D $\frac{a}{2} cos (\frac{π}{n})$
The area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
A $tan (\frac{π}{n}) : \frac{π}{n}$
B $cos (\frac{π}{n}) : \frac{π}{n}$
C $sin (\frac{π}{n}) : \frac{π}{n}$
D $cot (\frac{π}{n}) : \frac{π}{n}$
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be

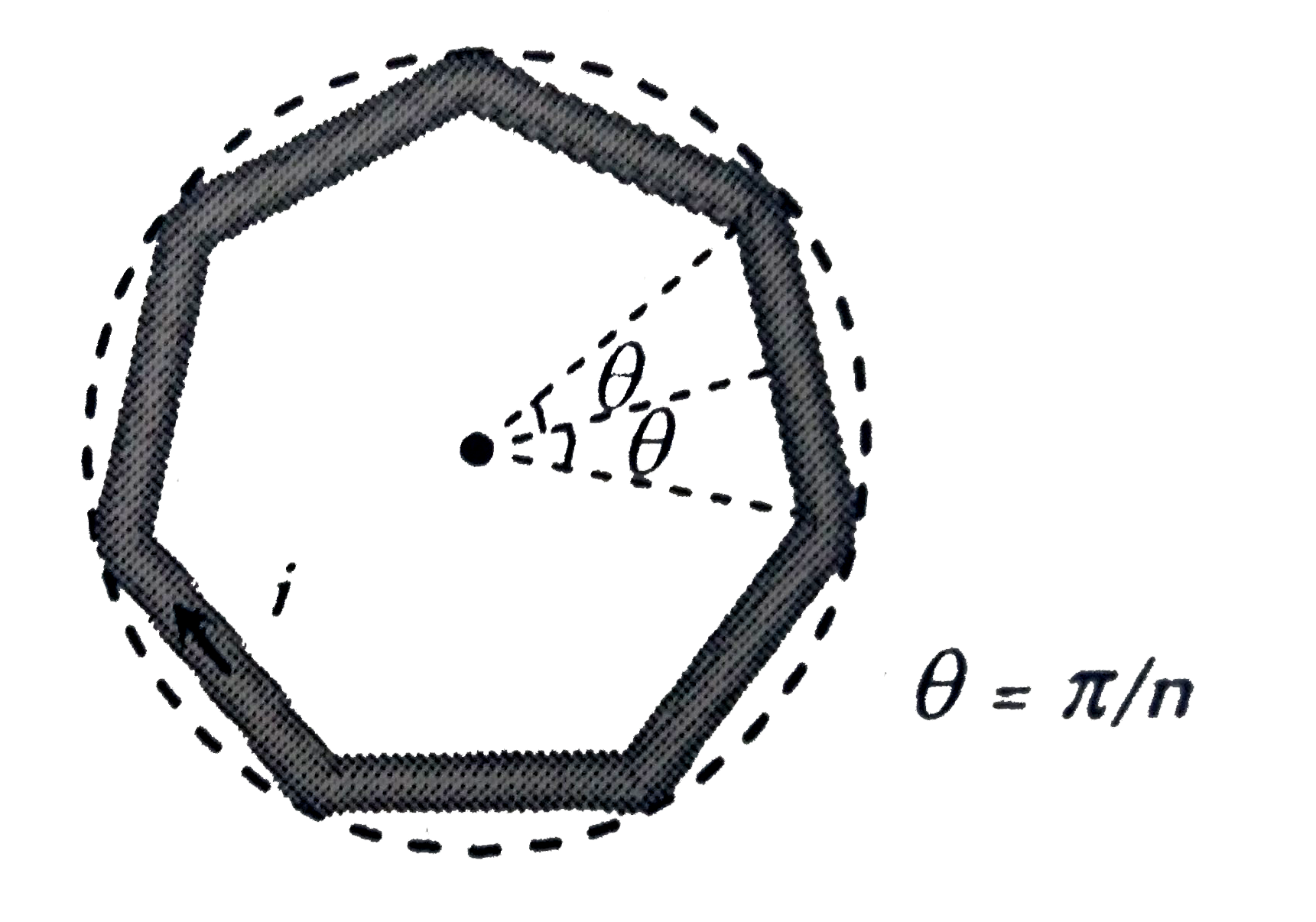A $\frac{μ_{0} i}{2 π a} tan \frac{π}{n}$
B $\frac{μ_{0} n i}{2 π a} tan \frac{π}{n}$
C $\frac{2}{π} \frac{n i}{a} μ_{0} tan \frac{π}{n}$
D $\frac{n i}{2 a} μ_{0} tan \frac{π}{n}$