In a triangle ABC, AB = 5 , BC = 7, AC = 6. A point P is in the plane such that it is at distance '2' units from AB and 3 units form AC then its distance from BC
is 12√6−287 when P is inside the trinagle
may be 12√6−87 when P is outside the triangle
may be 12√6+147 when P is inside the triangle
may be 12√6+147 when P is outside the triangle
The correct Answer is:A, B, C

a=7,b=6,c=5
∴s=9
∴Area Δ=√s(s−a)(s−b)(s−c)=6√6
Now, PF = 2, PE = x
Let PD = x
Then
Δ=12×2×5+12×x×7+12×3×6
∴6√6=5+7x2+9
∴x=12√6−287
When P lies outside the triangle

Area of ΔABC=12x×7+12×3×6−12×2×5
∴6√6=72x+9−5
∴x=12√6−87
Similarly, in one more case, we get 12√6+87
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Matrix)6videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Single)80videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank32videos
PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE
Similar Questions
Knowledge Check
- Question 1 - Select One
In right triangle, ABC, AB=10,BC=8,AC=6.
A35B34C45D54 - Question 2 - Select One
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
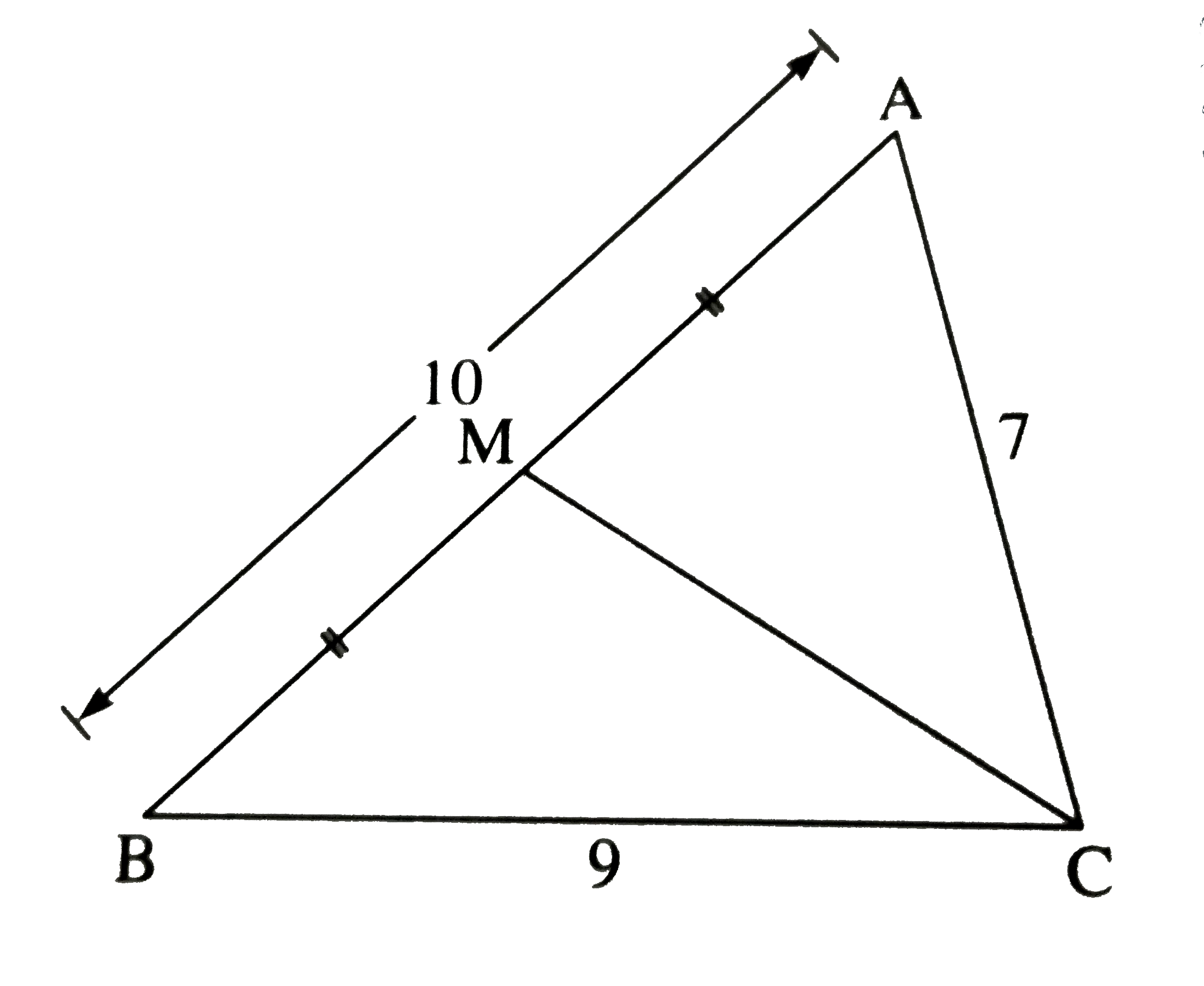
In △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
 View Solution
View SolutionIn a triangle ABC, if AB = 20 cm, AC = 21 cm and BC = 29 cm, then find the distance vertex A and mid point of BC.
View SolutionIn a ΔABC,AB=5cm,AC=7cm,BC=6cm, If AD⊥BC BC. Find the length of BD.
View SolutionConstruct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC=105∘. Hence
Construct the locus of points equidistant from BA and BC.View SolutionTriangle ABC is isosceles with AB=ACandBC=65cm. P is a point on BC such that the perpendiculardistances from P to ABandAC are 24cmand36cm, respectively. The area of triangle ABC (in sq cm is)
View SolutionIn ΔABC,AB=10,AC=7,BC=9 then find the length of the medium drawn point C to side AB .
View Solution

