Let ABCDEFGHIJKL be a regular dodecagon. Then the value of ABAF+AFAB is equal to ____
Text Solution
The correct Answer is:4
AM=Rsin.π12orABsin.π12
Similarly, AN=Rsin.5π12⇒AF=2Rsin.5π12

∴ABAF+AFAB=sin.π12sin.5π12+sin.5π12sin.π12
=tan.π12+cot.π12
=(2−√3)+(2+√3)=4
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Main Previous Year
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Advanced Previous Year
11 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Matrix)
6 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
If ABCDEF is a regular hexagon , then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF =A4¯¯¯¯¯¯ADB3¯¯¯¯¯¯ADC2¯¯¯¯¯¯ADD¯¯¯¯¯¯ADABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
A2−−→AOB2−−→AOC6−−→AOD0If ABCDEF is a regular hexagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=
A¯¯¯¯¯¯ADB3¯¯¯¯¯¯ADC2¯¯¯¯¯¯ADD¯¯¯O
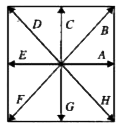
A number of vectors are as shown in .They can be combined in various ways , like →A+→C=→B . What is the value of (a) →E+→C (b) →A+→F (c ) →A+→D (d) →E+→A (e ) →A−→B .
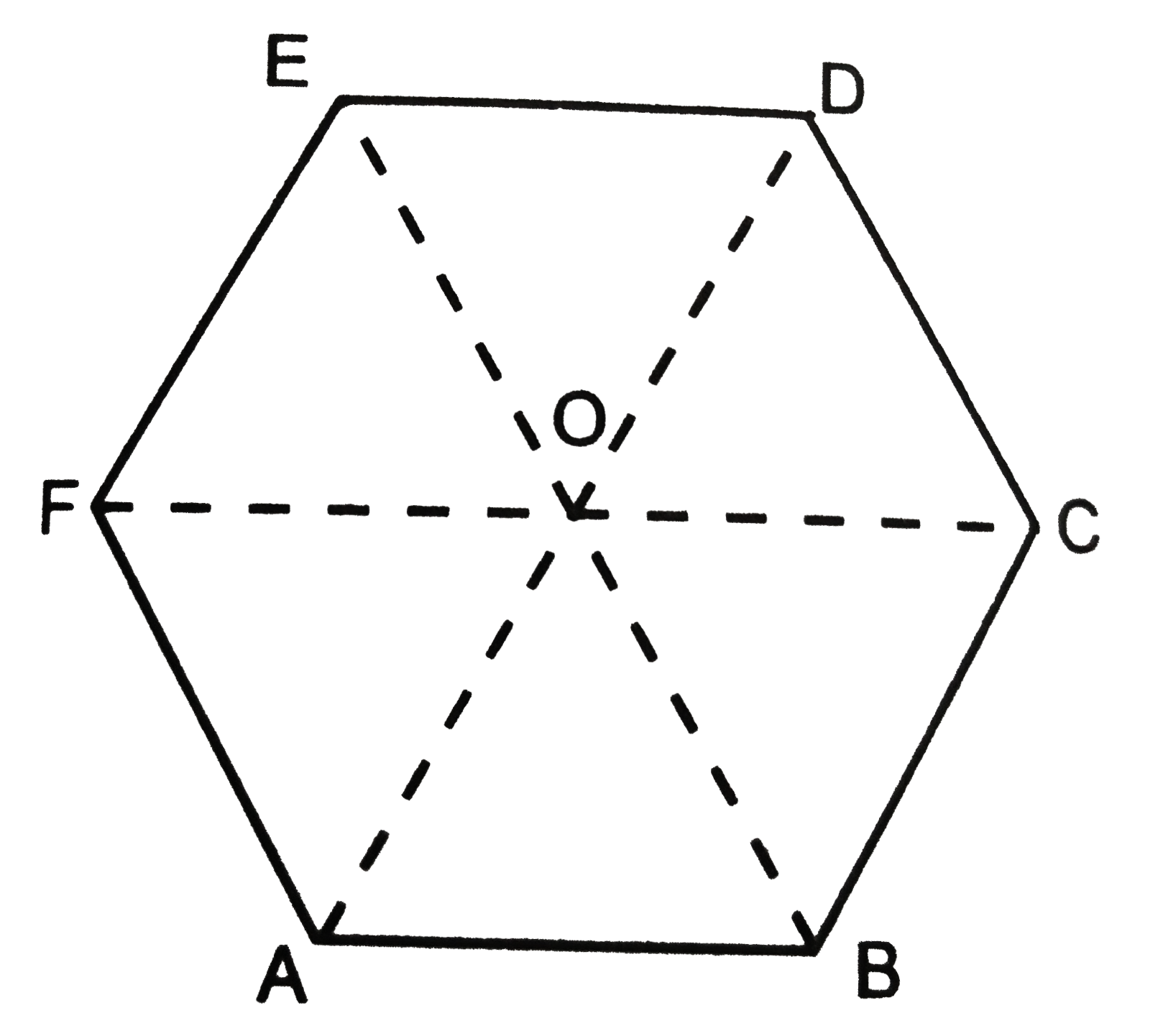
View SolutionIf ABCDEF is a regular hexagon inscribed in a circle with centre O, then the value of ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF equals
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionIf ABCDEF is a regular hexagon and AB+AC+AD+AE+AF=λAD then λ is equal to
View Solution

 .
.