A circle is inscribed in an equilateral triangle of side a. Find the area of any square inscribed in this circle.
To find the area of a square inscribed in a circle that is inscribed in an equilateral triangle of side a, we can follow these steps:
Step 1: Find the radius of the inscribed circle (inradius)
For an equilateral triangle with side length a, the formula for the inradius r is given by:
r=a2√3
Step 2: Understand the square inscribed in the circle
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. The diameter D of the circle is:
D=2r=2×a2√3=a√3
Step 3: Relate the side of the square to the diameter
Let the side of the square be s. The relationship between the side of the square and the diameter of the circle is given by the formula:
s√2=D
Substituting the value of D:
s√2=a√3
Step 4: Solve for the side of the square
To find s, we rearrange the equation:
s=a√3√2=a√6
Step 5: Calculate the area of the square
The area A of the square is given by:
A=s2=(a√6)2=a26
Final Answer
Thus, the area of the square inscribed in the circle is:
a26
---
For an equilateral triangle with side length a, the formula for the inradius r is given by:
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. The diameter D of the circle is:
Let the side of the square be s. The relationship between the side of the square and the diameter of the circle is given by the formula:
To find s, we rearrange the equation:
The area A of the square is given by:
Thus, the area of the square inscribed in the circle is:
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.18videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.28videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle is inscribed in an equilateral triangle of side a. What is the area of any square inscribed in the circle ?
Aa23Ba24Ca26Da28 - Question 2 - Select One
A circle is cirumscribed in an equilateral triangle of side 'l'. The area of any square inscribed in the circle is :
A43l2B23l2C13l2Dl2 - Question 3 - Select One
A circle is inscribed in a equilateral triangle of side 24 cm. What is the area ( in cm2 ) of a square inscribed in the circle ?
A48B72C54D96
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is ______.
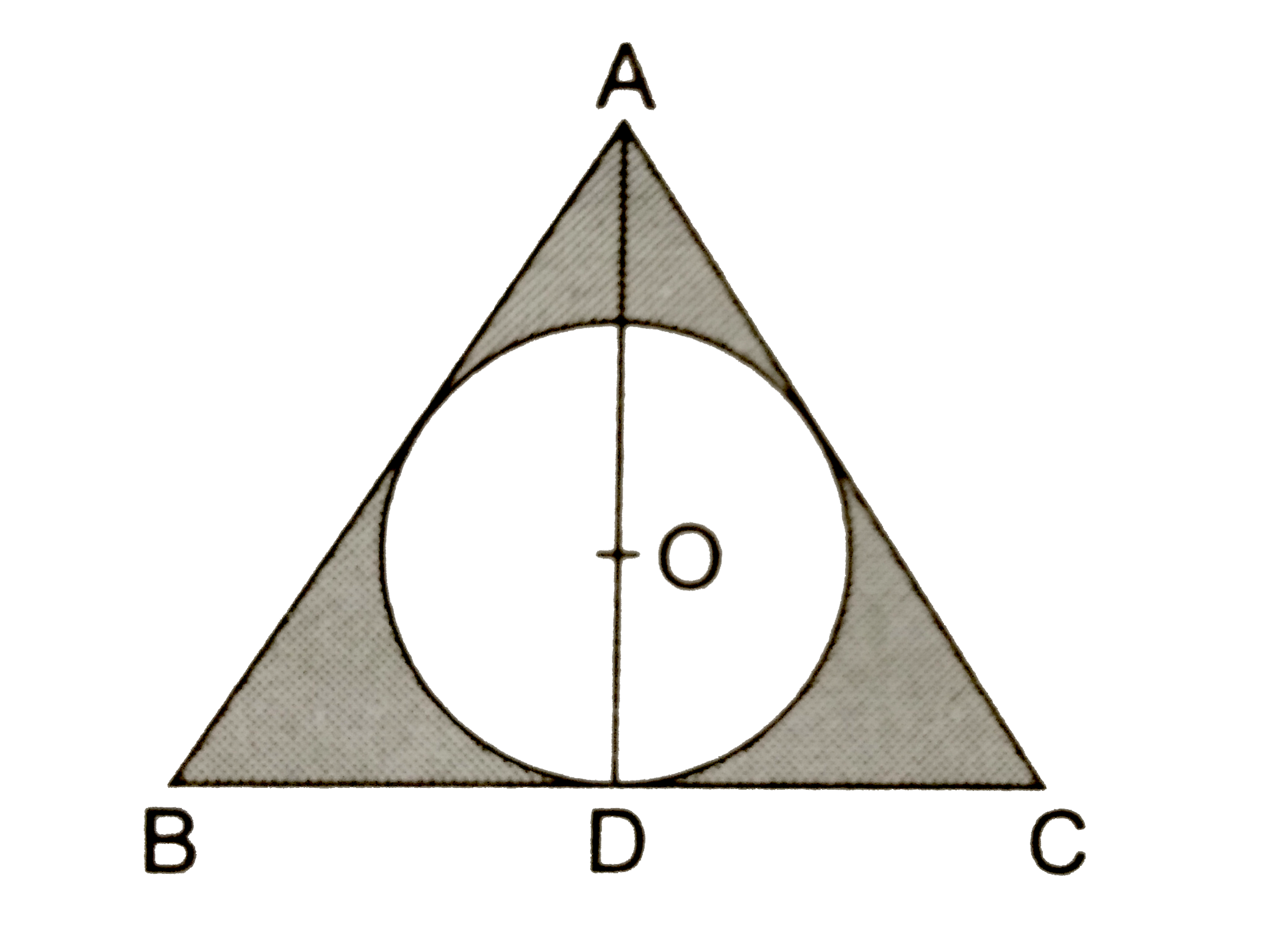
View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
 View Solution
View SolutionA circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View SolutionThe area of circle inscribed in an equilateral triangle of side 12 cm is
View SolutionThe area of circle inscribed in an equilateral triangle of side 12 cm is
View Solution

