find the height of the regular pyramid with each edge measuring l cm.
Also,
(i) if $α$ is angle between any edge and face not containing that edge, then prove that $cos α = \frac{1}{\sqrt{3}}$
(ii) if $β$ is the between the two faces, then prove that $cos β = \frac{1}{3}$

Video Solution

Text Solution

Verified by Experts

In the figure we have regular pyramid.

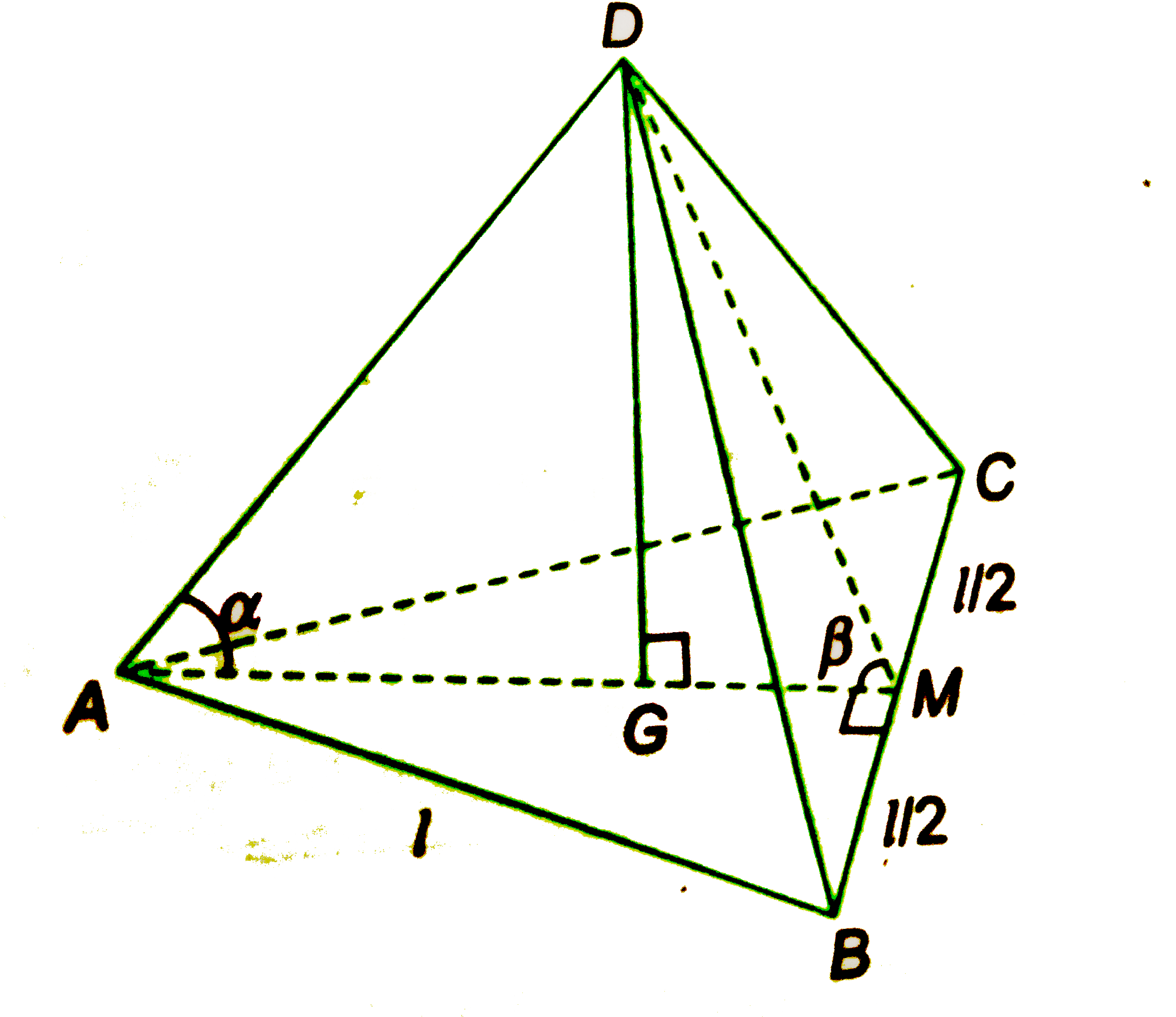
All the edges have length l cm.
So, each face of the pyramid is an equilateral triangle.
From vertex D drop perpendicular to meet opposite face ABC at point G, which is the centre of the triangle ABC.
Here, G is also centroid of triangle ABC as it an equailateral triangle.
Clearly, $A G = \frac{2}{3} A M$
In triangle $A M B, A M = A B {sin 60}^{\circ} = \frac{\sqrt{3}}{2} l c m$
$∴ A G = \frac{2}{3} \times A M = \frac{2}{3} \times \frac{\sqrt{3}}{2} l = \frac{1}{2 \sqrt{3}} lcm$
In triangle AGD, using Pythagoras, we get
$A D^{2} = A G^{2} + G D^{2}$
$∴ l^{2} = \frac{1}{3} l^{2} + G D^{2}$
$∴ G D = \sqrt{\frac{2}{3}} 1 c m$
For angle between any edge and face not containing that edge, consider edge AD and face ABC.
Angle between them is $α$ ,which is angle between AD and AM.
In triangle AGD, $cos α = \frac{A G}{A D} = \frac{\frac{1}{\sqrt{3}} l}{l} = \frac{1}{\sqrt{3}}$
Angle between two faces ABC and BCD is the angle between AM and DM, which is $β$ .
In triangle $D G M, cos β = \frac{G M}{D M} = \frac{1}{3}$

Updated on:21/07/2023

The total surface area of a regular triangular pyramid with each edge of length 1 cm is
A $4 \sqrt{3} c m^{2}$
B $\frac{4}{3} \sqrt{3} c m^{2}$
C $\sqrt{3} c m^{2}$
D $4 c m^{2}$
Comprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors $\to a, \to b$ and $\to c$ respectively of the regular tetrahedron.
The angle between any edge and a face not containing the edge is
A ${cos}^{- 1} (\frac{1}{2})$
B ${cos}^{- 1} (\frac{1}{4})$
C ${cos}^{- 1} (\frac{1}{\sqrt{3}}$
D ${cos}^{- 1} (\frac{\sqrt{3}}{2})$
Comprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors $\to a, \to b$ and $\to c$ respectively of the regular tetrahedron.
The angle between any two faces is
A ${cos}^{- 1} (\frac{1}{\sqrt{2}})$
B ${cos}^{- 1} (\frac{1}{4})$
C ${cos}^{- 1} (\frac{\sqrt{3}}{2})$
D ${cos}^{- 1} (\frac{1}{2})$