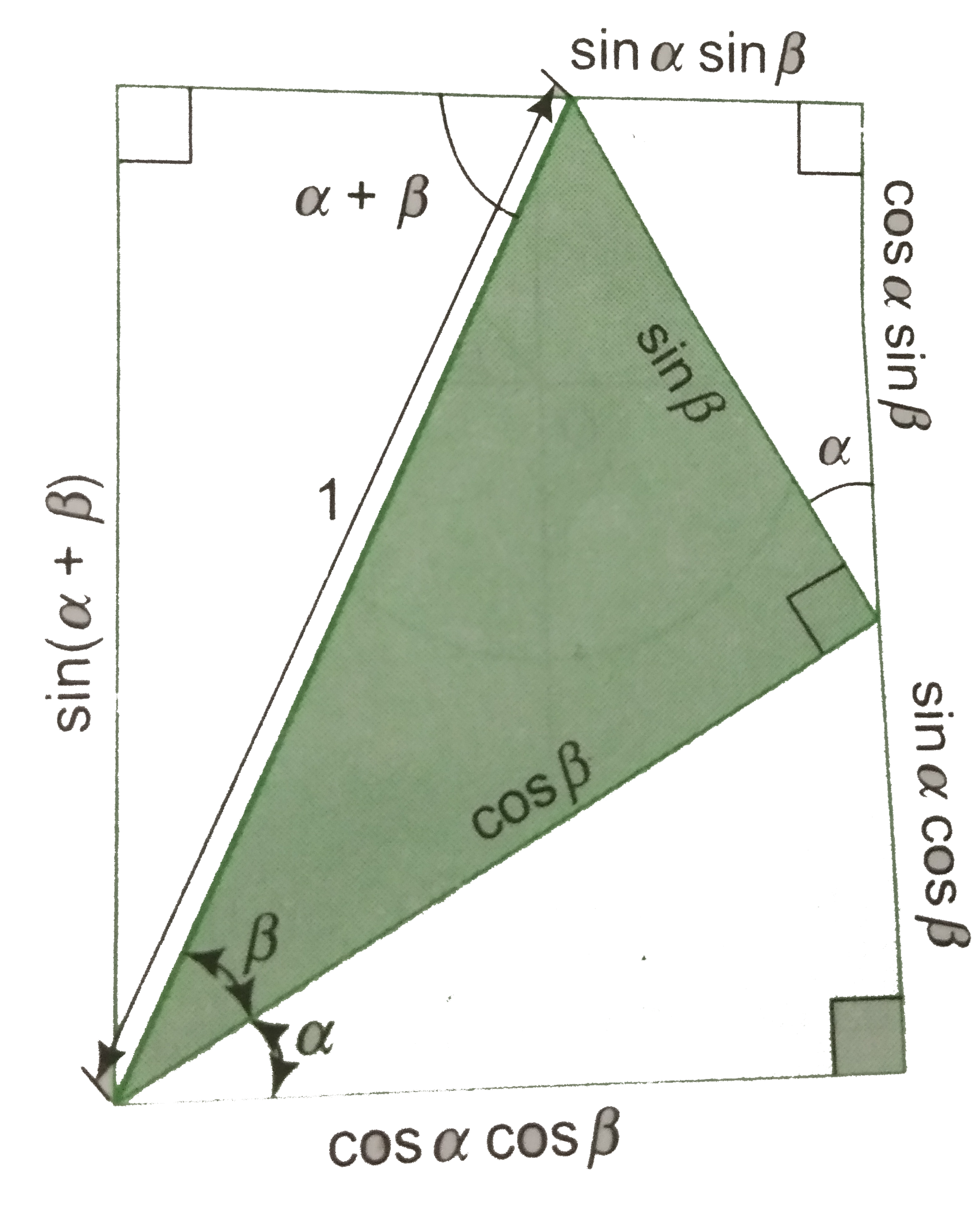
By geometrical interpretation, prove that
(i) $sin (α + β) = sin α cos β + sin β cos α$
(ii) $cos (α + β) = cos α cos β - sin α sin β$

Video Solution

Text Solution

Verified by Experts

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.1
8videos
TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.2
8videos
TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1videos
TRIGONOMETRIC EQUATIONS
BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS

Similar Questions

Knowledge Check

Question 1 - Select One
$\frac{cos α + cos β}{sin α - sin β} + \frac{sin α + sin β}{cos α - cos β}$ =
A1
B2
C $\sqrt{2}$
D0
Question 2 - Select One
$2 {sin}^{2} β + 4 cos (α + β) sin α sin β + cos 2 (α + β) =$
A $sin 2 α$
B $cos 2 β$
C $cos 2 α$
D $sin 2 β$

CENGAGE-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile