For acute angle $θ$ , Prove that $sin θ < θ < tan θ$ .

Video Solution

Text Solution

Verified by Experts

Consider the circle with unit radius as show in the following figure.
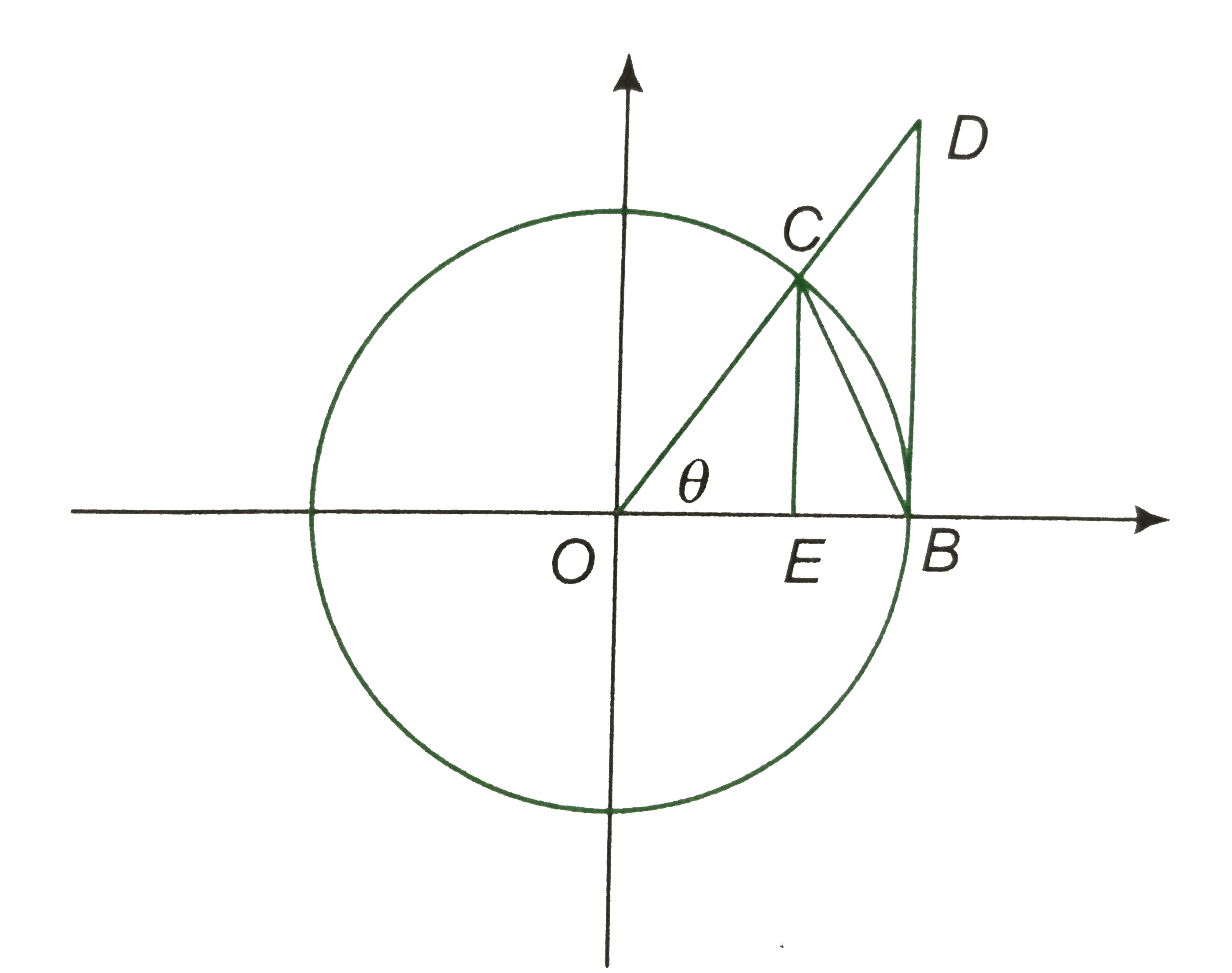From the figure, from position of C on the circle
Area of $Δ O B C < Area of sector Δ O B D$
$∴ \frac{1}{2} (C E) (O B) < \frac{1}{2} θ < \frac{1}{2} (O B) (B D)$
$\Rightarrow \frac{1}{2} (sin θ) (1) < \frac{1}{2} θ < \frac{1}{2} (1) (tan θ)$
$\Rightarrow sin θ < θ < tan θ$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $θ and 2 θ - 45^{\circ}$ are acute angles such that $sin θ = cos (2 θ - 45^{\circ})$ then $tan θ$ is
A1
B-1
C $\sqrt{3}$
D $\frac{1}{\sqrt{3}}$
Question 2 - Select One
For which acute angle $θ, {cosec}^{2} θ = 3 \sqrt{3} cot θ - 5$ ?
A $\frac{5 π}{12}$
B $\frac{π}{3}$
C $\frac{π}{6}$
D $\frac{π}{4}$

CENGAGE-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile