The number of values of x in the interval [0,5π] satisfying the equation.
3sin2x−7sinx+2=0 is-

A

0

B

5

C

6

D

10

Text Solution
Verified by Experts

The correct Answer is:c

3sin2x−7sinx+2=0
⇒(3sinx−1)(sinx−2)=0
∴sinx≠2
⇒sinx=13=sinα (say)
Where α is the least positive value of x
such that sinα=13
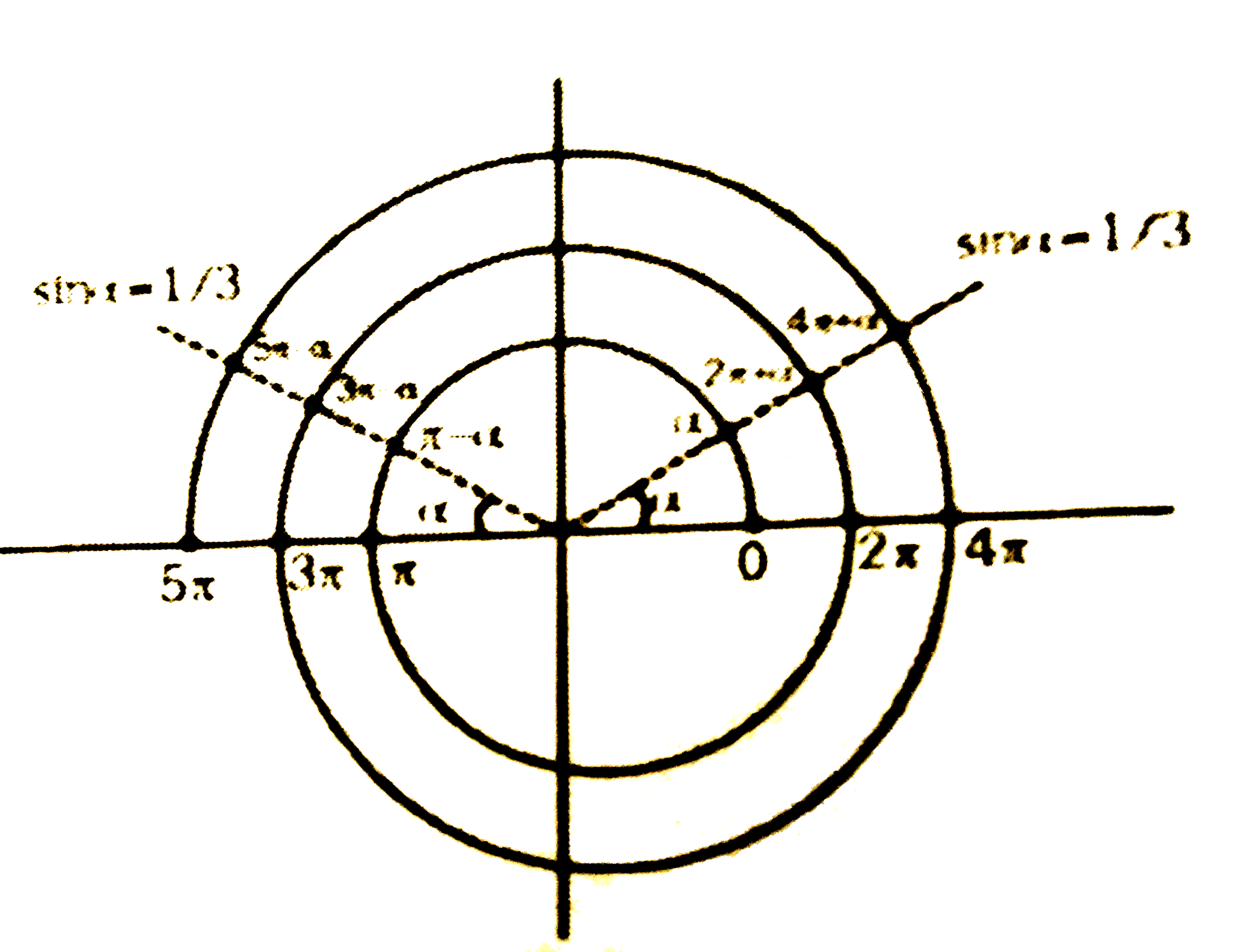
ocr_image
Clearly, 0<α<π2. We get the solution,
x=α,π−α,2π+α,4π+α and 5π−α
Hence total six values in [0,5π] Ans.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11MATHSLOGARITHM AND ITS APPLICATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The number of values of x in the interval [0,3π] satisfying the equation 3sin2x−7sinx+2=0 is

    A0
    B5
    C4
    D10

  • The number of values of x in the interval [0,5π] satisfying the equation 3sin2x−7sinx+2=0 is

    A0
    B5
    C6
    D10

  • The number of values of x in the interval [0,5π] satisfying the equation 3sin2x−7sinx+2=0 is

    A0
    B4
    C6
    D10