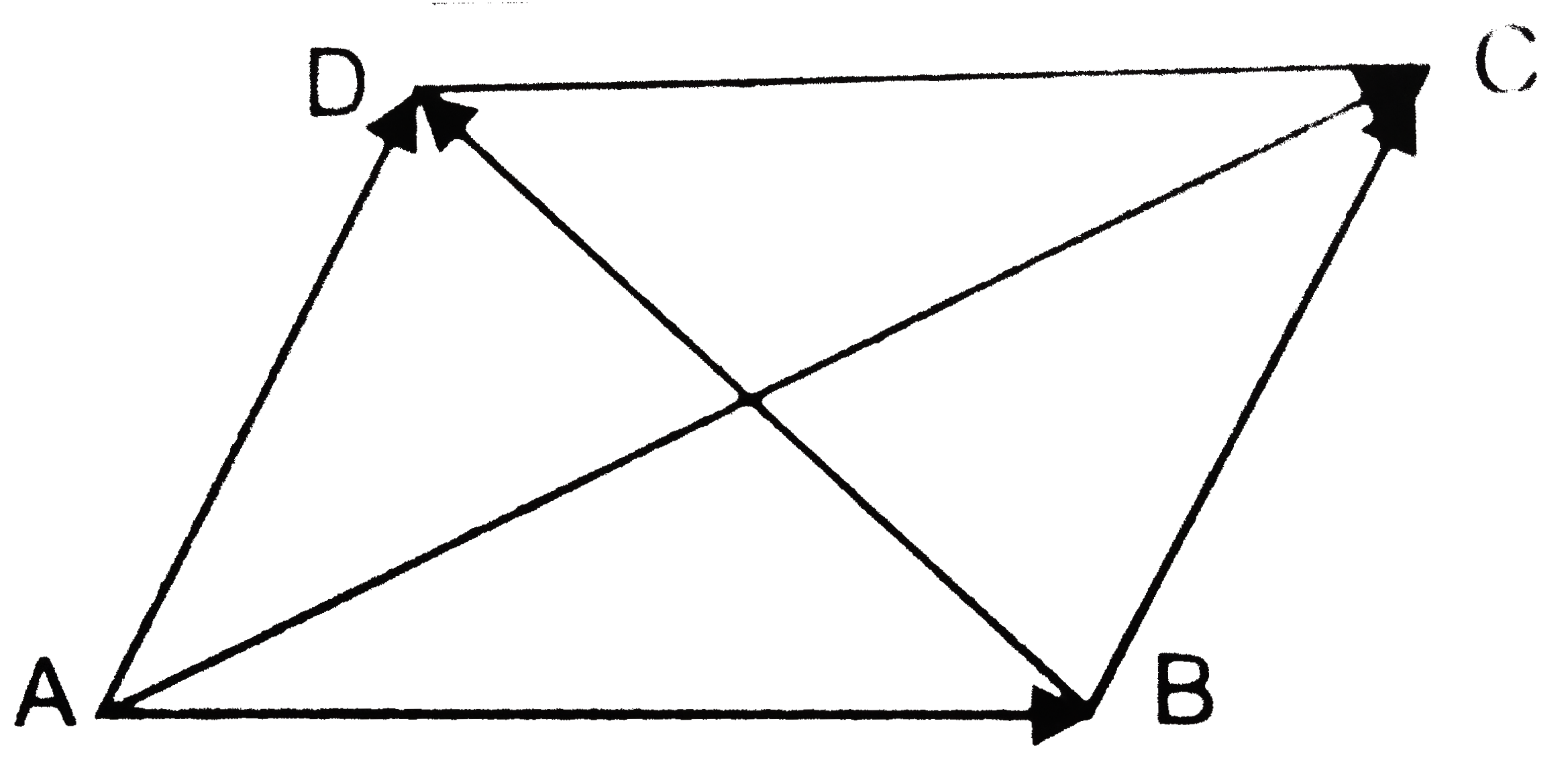
A parallelogram ABCD. Prove that $- - \to A C + - - \to B D = 2 - - \to B C$ '

Video Solution

Text Solution

Generated By DoubtnutGPT

To prove that $\to A C + \to B D = 2 \to B C$ in a parallelogram ABCD, we will follow these steps:
Step 1: Define the vectors
In a parallelogram ABCD, we can define the vectors as follows:
- Let $\to A B = \to u$
- Let $\to B C = \to v$
From the properties of a parallelogram, we know:
- $\to A D = \to u$ (since opposite sides are equal)
- $\to D C = \to v$ (since opposite sides are equal)
Step 2: Express $\to A C$ and $\to B D$ in terms of $\to u$ and $\to v$
Using the vector addition:
- $\to A C = \to A B + \to B C = \to u + \to v$
- $\to B D = \to B C + \to D C = \to v + \to u = \to u + \to v$
Step 3: Add the vectors $\to A C$ and $\to B D$
Now, we can add the two vectors:
$\to A C + \to B D = (\to u + \to v) + (\to u + \to v) = 2 \to u + 2 \to v$
Step 4: Factor out the common terms
We can factor out the 2:
$\to A C + \to B D = 2 (\to u + \to v)$
Step 5: Recognize that $\to u + \to v = \to B C$
Since $\to B C = \to v$ , we can write:
$\to A C + \to B D = 2 \to B C$
Conclusion
Thus, we have proven that:
$\to A C + \to B D = 2 \to B C$

Updated on:7/8/2024