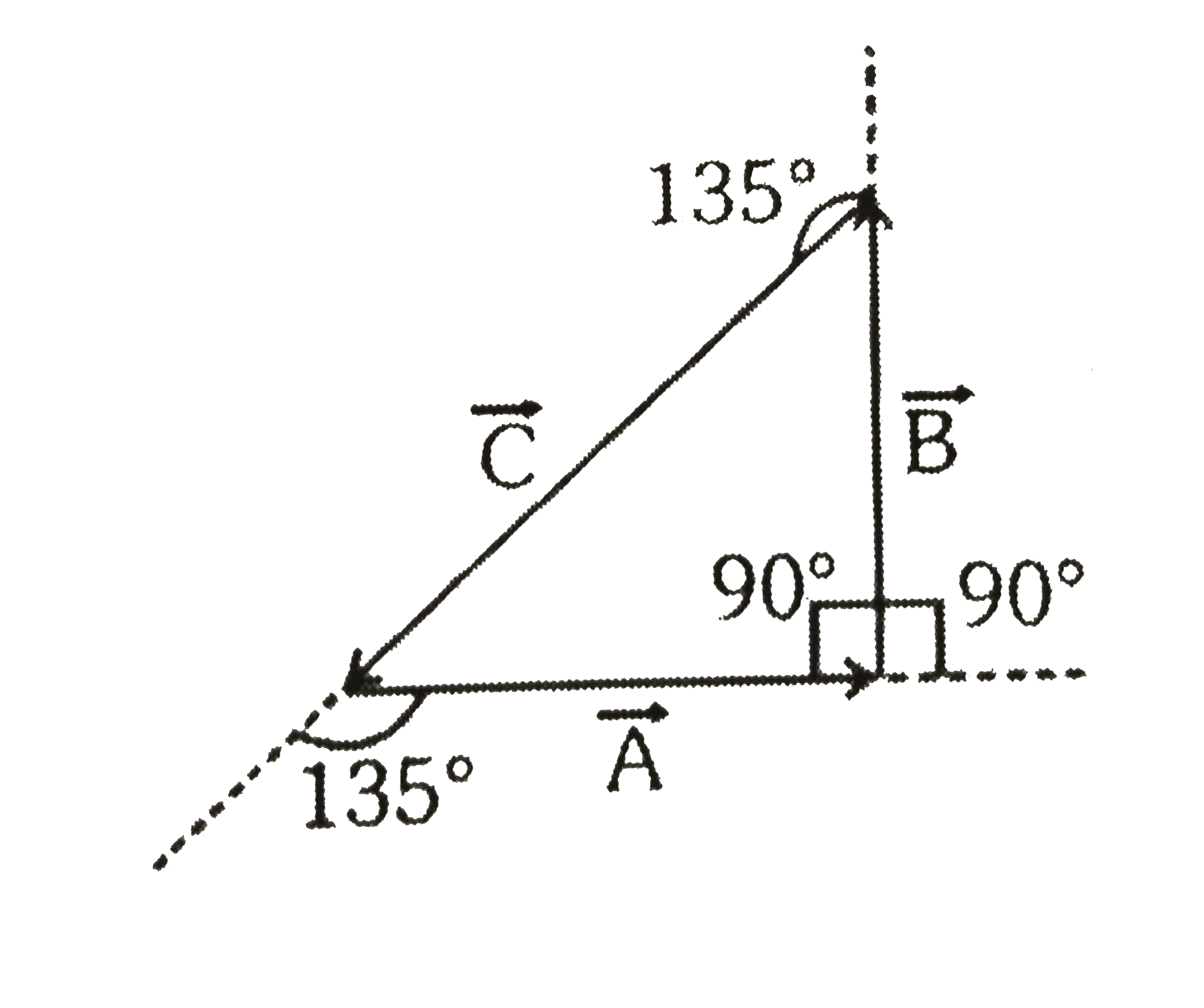
Given that $\to A + \to B + \to C = 0$ , out of three vectors two are equal in magnitude and the magnitude of third vector is $\sqrt{2}$ times that of either of two having equal magnitude. Then angle between vectors are given by

$30^{\circ}, 60^{\circ}, 90^{\circ}$

$45^{\circ}, 45^{\circ}, 90^{\circ}$

$45^{\circ}, 60^{\circ}, 90^{\circ}$

$90^{\circ}, 135^{\circ}, 135^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

given that $\to A + \to B + \to C = 0$ out of three vectors two are equal in magnitude and the magnitude of third vector is $\sqrt{2}$ times that of either of the two having equal magnitude. Then the angles between vectors are given by
A $30^{\circ}$ , $60^{\circ}$ , $90^{\circ}$
B $40^{\circ}$ , $45^{\circ}$ ,90^@
C $45^{\circ}$ , $60^{\circ}$ , $90^{\circ}$
D $90^{\circ}$ , $135^{\circ}$ , $135^{\circ}$
Given that P+Q+R= 0. Two out of the three vectors are equal in magnitude. The magnitude fo the third vector is s $\sqrt{2}$ times that of the other two. Which of the following can be the angles between these vectors?
A $90^{\circ}$
B $45^{\circ}, 45^{\circ}, 90^{\circ}$
C $30^{\circ}, 60^{\circ}, 90^{\circ}$
D $45^{\circ}, 90^{\circ}, 135^{\circ}$
If A and B are two non- zero vectors having equal magnitude, then angle between the vectors A and $A - B$ is
A $0^{\circ}$
B $90^{\circ}$
C $180^{\circ}$
Ddependent on the orientation of A and B