3/4 th of first order reaction was completed in 32 min, 15/16 the part will be completed in
24 min
64 min
16 min
32 min
The correct Answer is:B
To solve the problem of how long it will take for 1516 of a first-order reaction to be completed, given that 34 of the reaction was completed in 32 minutes, we can follow these steps:
Step 1: Understand the first-order reaction kinetics
For a first-order reaction, the rate constant k can be determined using the formula:
k=2.303tlog(A0A0−x)
where:
- A0 is the initial concentration,
- x is the amount reacted,
- t is the time taken.
Step 2: Calculate the value of k
Given that 34 of the reaction is completed in 32 minutes, we can set:
- A0=1 (initial concentration),
- x=34.
Thus, the concentration remaining A=A0−x=1−34=14.
Now substituting into the equation:
k=2.30332log(11/4)=2.30332log(4)
Since log(4)=log(22)=2log(2) and log(2)≈0.301:
log(4)=2×0.301=0.602
Now substituting this back into the equation for k:
k=2.30332×0.602≈0.043 min−1
Step 3: Calculate the time for 1516 of the reaction to be completed
Now we need to find the time taken for 1516 of the reaction to be completed. Here:
- A0=1,
- x=1516,
- Remaining concentration A=A0−x=1−1516=116.
Using the first-order reaction formula again:
t=2.303klog(A0A0−x)=2.3030.043log(11/16)
Calculating log(16):
log(16)=log(24)=4log(2)≈4×0.301=1.204
Now substituting this back into the time equation:
t=2.3030.043×1.204≈64 minutes
Final Answer
Thus, the time taken for 1516 of the reaction to be completed is 64 minutes.
---
For a first-order reaction, the rate constant k can be determined using the formula:
k=2.303tlog(A0A0−x)
where:
- A0 is the initial concentration,
- x is the amount reacted,
- t is the time taken.
Given that 34 of the reaction is completed in 32 minutes, we can set:
- A0=1 (initial concentration),
- x=34.
k=2.30332log(11/4)=2.30332log(4)
Since log(4)=log(22)=2log(2) and log(2)≈0.301:
log(4)=2×0.301=0.602
Now substituting this back into the equation for k:
k=2.30332×0.602≈0.043 min−1
Now we need to find the time taken for 1516 of the reaction to be completed. Here:
- A0=1,
- x=1516,
- Remaining concentration A=A0−x=1−1516=116.
t=2.303klog(A0A0−x)=2.3030.043log(11/16)
Calculating log(16):
log(16)=log(24)=4log(2)≈4×0.301=1.204
Now substituting this back into the time equation:
t=2.3030.043×1.204≈64 minutes
Thus, the time taken for 1516 of the reaction to be completed is 64 minutes.
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (MOLECULARITY)
5 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (HALF-LIFE)
7 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (RATE OF REACTION & FACTORS)
14 Videos
- CARBOXYLIC ACIDBOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions
288 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS
10 Videos
Similar Questions
Molecularity of the following elementary reactions 2NO+O2→2NO2
View Solution……………………… reaction obeys the expresison t1/2=1/ka in chemical kinetics.
View SolutionThe rate of a gaseous reaction is given by the expression k [A] [B]. If the volume of the reaction vessel is suddenly reduced to 1/4th of the initial volume, the reaction rate relating to original rate will be
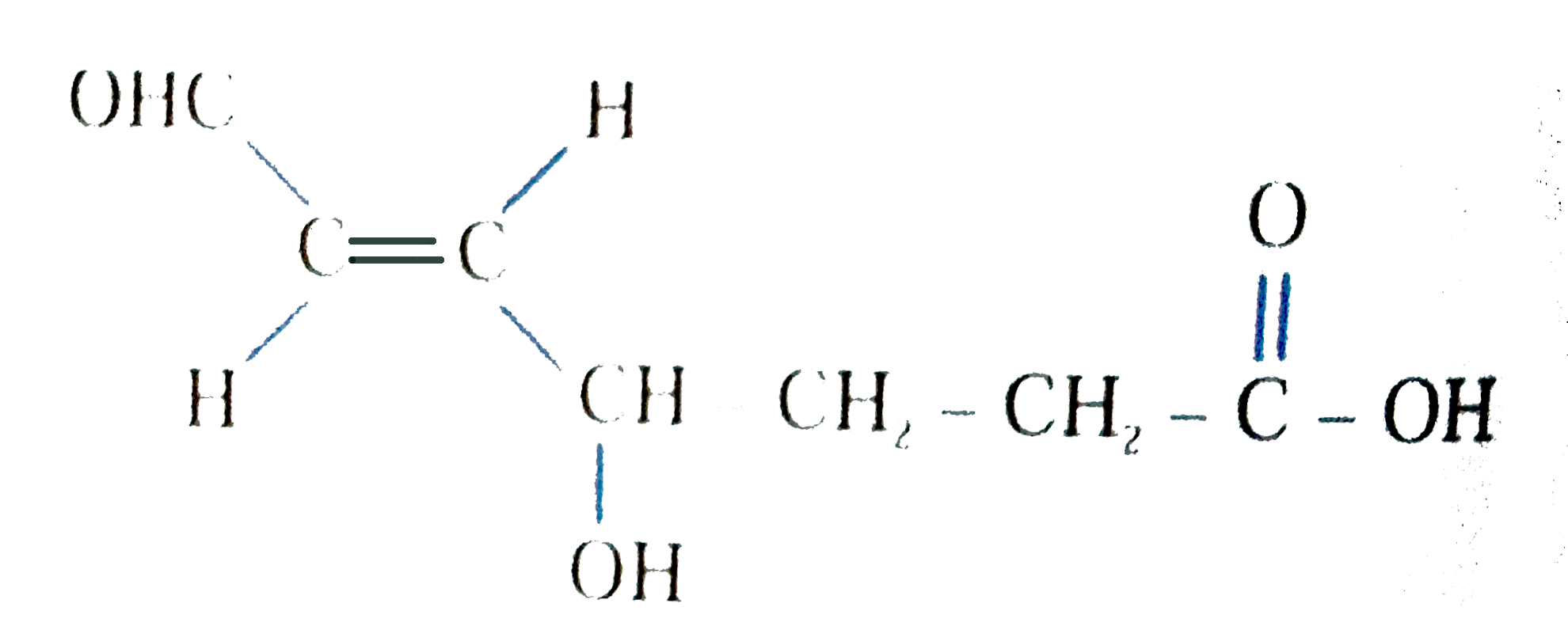
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionIf 75% of a frist-order reaction is completed in 32 min, than 50% of the reaction would complete in? a. 24 min b. 16 min c. 8 min d. 4 min
View Solution75% of a first order reaction was completed in 32 min. When was 50% of the reaction completed ?
View Solution75% of a first order reaction was completed in 32 min. When was 50% of the reaction completed ?
View SolutionIf 75% of first order reaction is completed in 32 min, then 50% of the reaction would be complete in:
View Solution75% of a first order reaction is completed in 32 min. 50% of the reaction would have been completed in
View Solution75% of the first order reaction completed in 3 min. 50% of the reaction was completed in
View SolutionIf 75% of first order reaction is completed in 32 min, then 50% of the reaction would be complete in:
View Solution3/4 th of first order reaction was completed in 32 min 15/16 the part will be completed in
View Solution99% of a first order reaction was completed in 32 in. When wil 99.9% of the reaction complete?
View Solution75% of a first order reaction was completed in 32 min. When would 50% of the reaction be completed ?
View Solution
