The rate temperature changes from 300K to 310K. Activation energy of such a reaction will be (R=8.314JK−1mol−1 and log2=0.3010)
48.6kJmol−1
58.5kJmol−1
60.5kJmol−1
53.6kJmol−1
The correct Answer is:D
To find the activation energy (Ea) for the reaction when the temperature changes from 300 K to 310 K, we can use the Arrhenius equation in the form of the logarithmic relationship:
logk2k1=−Ea2.303R(1T2−1T1)
Step 1: Identify the known values
- T1=300K
- T2=310K
- R=8.314JK−1mol−1
- The temperature coefficient states that when the temperature increases by 10 K, the rate constant doubles, thus k2=2k1.
Step 2: Calculate k2k1
Since the rate constant doubles when the temperature increases by 10 K:
k2k1=2
Step 3: Substitute values into the equation
Substituting the values into the logarithmic equation:
log2=−Ea2.303×8.314(1310−1300)
Step 4: Calculate 1T2−1T1
Calculating the difference:
1310−1300=300−310310×300=−1093000=−19300
Step 5: Substitute log2 and calculate Ea
Using log2=0.3010:
0.3010=−Ea2.303×8.314(−19300)
This simplifies to:
0.3010=Ea2.303×8.314×9300
Step 6: Solve for Ea
Rearranging gives:
Ea=0.3010×2.303×8.314×9300
Calculating the right-hand side:
1. Calculate 2.303×8.314≈19.156
2. Then calculate 19.156×9300≈178,000
3. Finally, multiply by 0.3010:
Ea≈0.3010×178,000≈53598J/mol
Step 7: Convert to kilojoules
To convert to kilojoules:
Ea≈535981000≈53.598kJ/mol
Final Answer
The activation energy Ea is approximately:
53.6kJ/mol
- T1=300K
- T2=310K
- R=8.314JK−1mol−1
- The temperature coefficient states that when the temperature increases by 10 K, the rate constant doubles, thus k2=2k1.
Since the rate constant doubles when the temperature increases by 10 K:
k2k1=2
Substituting the values into the logarithmic equation:
log2=−Ea2.303×8.314(1310−1300)
Calculating the difference:
1310−1300=300−310310×300=−1093000=−19300
Using log2=0.3010:
0.3010=−Ea2.303×8.314(−19300)
0.3010=Ea2.303×8.314×9300
Rearranging gives:
Ea=0.3010×2.303×8.314×9300
1. Calculate 2.303×8.314≈19.156
2. Then calculate 19.156×9300≈178,000
3. Finally, multiply by 0.3010:
Ea≈0.3010×178,000≈53598J/mol
To convert to kilojoules:
Ea≈535981000≈53.598kJ/mol
The activation energy Ea is approximately:
53.6kJ/mol
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (C.W) ORDER OF REACTION
16 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (C.W) HALF LIFE
4 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (H.W) COLLISION THEORY
4 Videos
- CARBOXYLIC ACIDBOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions
288 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS
10 Videos
Similar Questions
The decomposition of CH3OH occurs as CH3CHO(g)→CH4(g)+CO(g), the kinetic data provided is

The rate expression thus can be given as
View SolutionThe half life period of a first order reaction is 10 minutes . The time required for the concentration of the reactant to change from 0.08 M to 0.02is :
View SolutionConsider the energy profile, for the reaction x+y→R+S .Which of the following deduction about reaction is not correct?

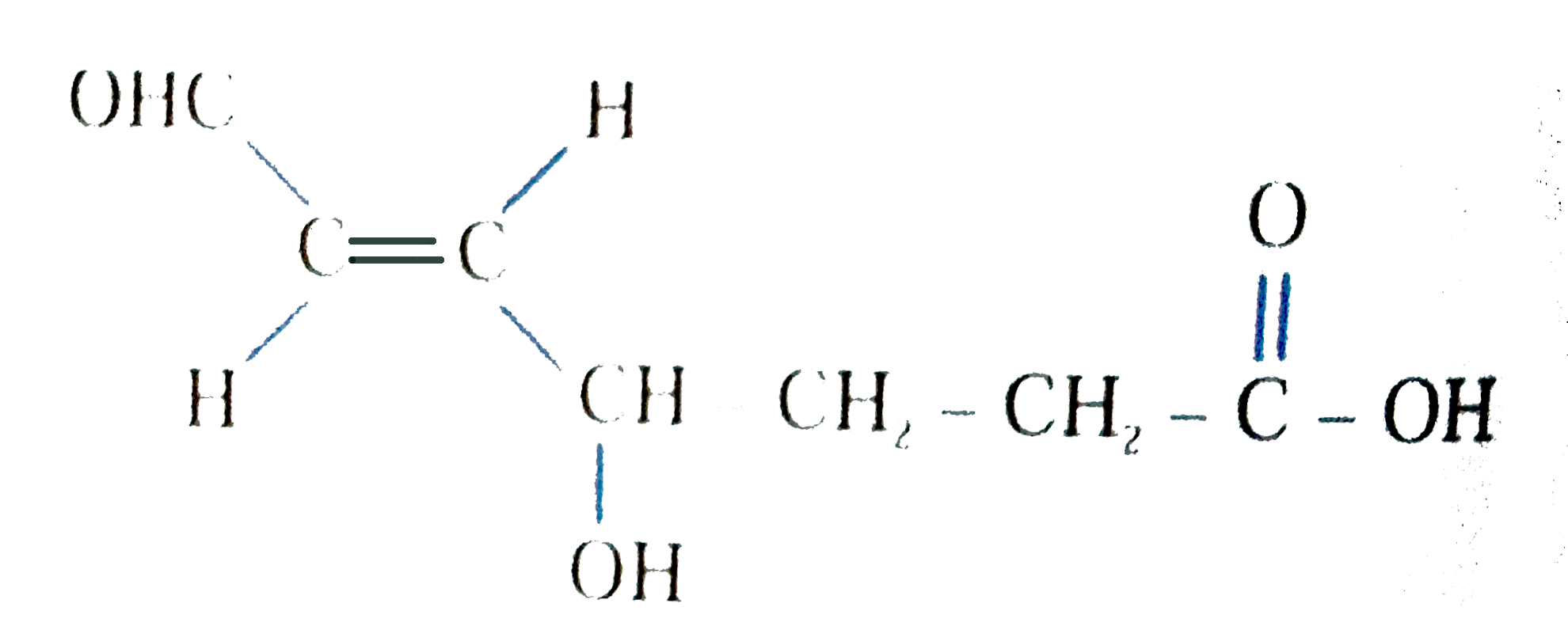
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionThe rate of a reaction doubles when its temperature changes form 300K to 310K. Activation energy of such a reaction will be:
(R=8.314JK−1mol−1andlog2=0.301)
View SolutionThe rate of a reaction doubles when the tempeature changes from 300 K to 310 K. Activation energy for the reaction is: (R = 8.314 JK^(-1) mol^(-1), log2 = 0.3010)
View Solutionकिसी अभिक्रिया की सक्रियण ऊर्जा 50kJmol−1 है , तो सिद्ध कीजिए की ताप 300K से 310K करने पर अभिक्रिया दर दोगुनी हो जाती है ।
View SolutionThe rate of a reaction doubles when its temperature changes from 300K to 310K . Activation energy of such a reaction will be - (R=8.314J.K−1mol−1andlog2=0.310)
View Solutionएक अभिक्रिया की दर दोगुनी हो जाती है, जब इसका ताप 300K से 310K हो जाता है। ऐसी अभिक्रिया की सक्रियण ऊर्जा होगी-(R= 8.314JK(-1)mol^(-1), log2=0.3010)
View Solutiona) The rate of a particular reaction doubles when the temperature changes from 300 K to 310 K. Calculate the energy of activation of the reaction. [Given : R=8.314 JK−1 mol−1].
View SolutionThe rate of a reaction doubles when its temperature changes from 300K to 310K. Activation energy of such a reaction will be:
(R=8.314JK−1mol−1andlog2=0.301)
View SolutionThe rate of a reaction doubles when its temperature changes from 300 K to 310 K.Activation energy of such a reaction will be:
(R=8.314 JK−1mol−1 and log 2=0.301)
View SolutionThe rate constant of a reaction is doubled when the temperature increased from 400K to 410K. Calculate the activation energy (Ea)
[R=8.314JK−1 mol−1] .
View SolutionThe temperature dependence of the rate of a chemical reaction can be explained by Arrhenius equation.The rate of a chemical reaction doubles for an increase of 10 K in absolute temperature from 300 K. Calculate the activation energy(Ea)? [ R=8.314 JK^(-1)mol^(-1),log 2 = 0.3010 ].
View Solution
