DDT on exposure to water decomposes according to first order kinetics. Half life = 10 years. How much time it will take for its decomposition to 99%?
50 years
66.6 years
500 years
666 years
The correct Answer is:B
To solve the problem of how long it will take for DDT to decompose 99% in water, we will follow these steps:
Step 1: Determine the rate constant (k)
The half-life (t₁/₂) of a first-order reaction is given as 10 years. The formula to calculate the rate constant (k) for a first-order reaction is:
k=0.693t1/2
Substituting the given half-life:
k=0.69310 years=0.0693 year−1
Step 2: Use the first-order kinetics formula
For a first-order reaction, the relationship between the amount of substance remaining and time is given by:
t=2.303klog(A0A)
Where:
- A0 is the initial amount of the substance.
- A is the amount of the substance remaining after time t.
Step 3: Calculate the amount remaining after 99% decomposition
If 99% of DDT has decomposed, then 1% remains. Therefore:
A=0.01A0
Step 4: Substitute values into the formula
Now, substituting A into the first-order kinetics formula:
t=2.3030.0693log(A00.01A0)
This simplifies to:
t=2.3030.0693log(10.01)
Calculating the logarithm:
log(10.01)=log(100)=2
Step 5: Calculate the time
Now substituting back into the equation:
t=2.3030.0693×2
Calculating the value:
t=2.303×20.0693≈4.6060.0693≈66.5 years
Conclusion
Thus, the time it will take for DDT to decompose 99% is approximately 66.5 years.
---
The half-life (t₁/₂) of a first-order reaction is given as 10 years. The formula to calculate the rate constant (k) for a first-order reaction is:
For a first-order reaction, the relationship between the amount of substance remaining and time is given by:
- A0 is the initial amount of the substance.
- A is the amount of the substance remaining after time t.
If 99% of DDT has decomposed, then 1% remains. Therefore:
Now, substituting A into the first-order kinetics formula:
Now substituting back into the equation:
Thus, the time it will take for DDT to decompose 99% is approximately 66.5 years.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (H.W) COLLISION THEORY7videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -339videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (H.W) (ORDER OF REACTION)16videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions288videos
CARBOXYLIC ACID
- BOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS10videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The reaction A→C has activation energy for the forward and the backward reaction has 25 kJ and 32 KJ respectively. The ΔH for the reaction is
05:45View SolutionA reaction proceeds by first order, 75% of this reactin was completed in 32 min. The time required for 50% completion is
04:14View SolutionRate expression for Xa+Yb→ products is Rate =K[A]m[B]n. Units of K w.r.t A and B respectively are s−1 and M−1s−1, when concentrations of A and B are increased by 4 times, then
02:16View SolutionProvide IUPAC name of the compound given below.
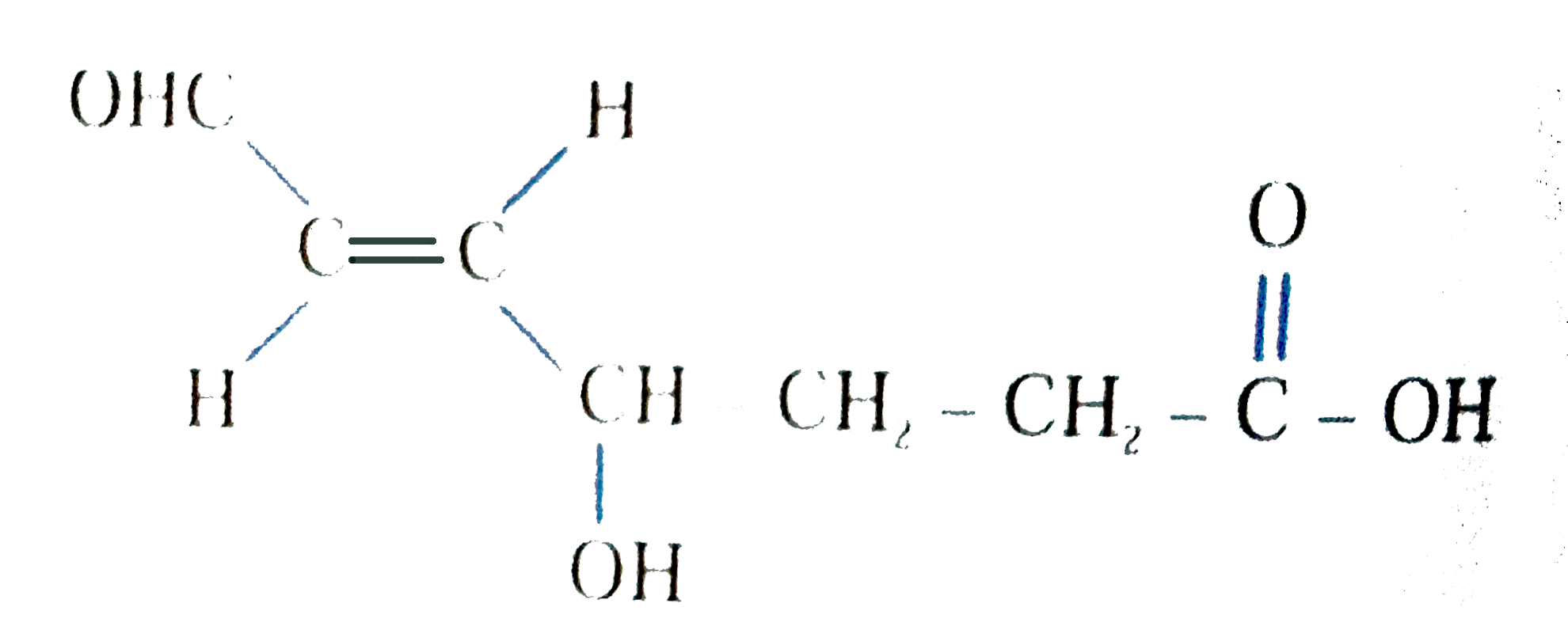 View Solution
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.03:09View SolutionA substance having a half-life period of 30 minutes decomposes according to the first order rate law. The fraction decomposed, the balance remaining after 1.5 hours and time for 60% decomposition on its doubling the initial concentration will be.
03:49View SolutionA first order reaction takes 10 minutes for 25% decomposition. Calculate half life period of the reaction.
03:31View SolutionHydrolysis of DDT is a first order reaction , its half life is 10 years . Time to hydrolyse 10 g DDT to half is
06:42View Solutionयदि किसी प्रथम कोटि की अभिक्रिया का अर्ध्द- आयुकाल 2 मिनट है तो इसके अपने मूल सान्द्रता के (i) 25% एवं (ii) 10% तक पहुँचने में कितना समय लगेगा।
02:39View SolutionThe thermal decomposition of a compound is of first order. If 50% of a sample of the compound is decomposed in 120 minutes, how long it take for 90% of the compounds to decompose.
05:09View SolutionThe half life of a first order reaction is 10 years . The time taken by 10 g of the reactant to reduce its half is ______.
04:10View SolutionFor a first order reactions, the half -life is 10 mins. How much time in minutes will it take to reduce the concentration of reactant to 25% of its original concentration ?
02:36View SolutionA first order reaction takes 46 min for its 99% completion . How much time did it take for its 75% completion -
04:21View SolutionDDT on exposure to water decomposes. How much time will it take for its 90% decomposition? (Half-life = 20 years)
03:58View SolutionThe half life of first order decomposition of nitramide is 2.0 hour at 15∘C.
NH2NO2(aq)→N2O(g)+H2O(l) If 6.2 gm of NH2NO2 is allowed to decompose, find :
time taken for nitramide to decompose 99%02:15View Solution

