Number of possible isomer for the complex [Co(en)2CI2]CI will be: (em = ethylenediamine)
A
3
B
4
C
2
D
1
Video Solution
Text Solution
The correct Answer is:A
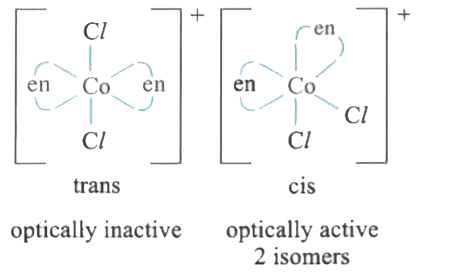
Total Isomers =1+2=3
|
Topper's Solved these Questions
- CO-ORDINATE COMPOUNDS BOOK - NARAYNACHAPTER - CO-ORDINATE COMPOUNDS EXERCISE - Exercise-4
60 Videos
- CO-ORDINATE COMPOUNDS BOOK - NARAYNACHAPTER - CO-ORDINATE COMPOUNDS EXERCISE - Exercise -2 (H.W.)
20 Videos
- CHEMISTRY OF HEAVY METALSBOOK - NARAYNACHAPTER - CHEMISTRY OF HEAVY METALSEXERCISE - Passage 13
1 Videos
- COORDINATION COMPLEXESBOOK - NARAYNACHAPTER - COORDINATION COMPLEXESEXERCISE - Compreshession type question
12 Videos
Similar Questions
Knowledge Check
Number of possible isomer for the complex [Co(en)2CI2]CI will be: (em = ethylenediamine)
A3B4C2D1Number of possible isomers for the complex [Co(en)2CI2] will be (en = ethylenediamine)
A3B4C2D1Number of possible isomers for the complex [Co(en)2CI2] CI will be: (en = ethylenediamine)
A3B4C2D1
Number of possible isomers for the complex [Co(en)2CI2] will be (en = ethylenediamine)
View SolutionHow many isomers are possible for the complex [Co(en)2Cl2](en=ethylene diamine )
View SolutionThe sum of coordination number and oxidation number of the metal M in the complex [M(en)2(C2O4)]CI (where en is ethylenediamine) is:
View SolutionThe sum of coordination number and oxidation number of the metal M in the complex [M(en)2(C2O4)]Cl (where en is ethylenediamine) is :
View SolutionThe sum of coordination number and oxidation number of the metal M in the complex [M(en)2(C2O4)]CI (where en is ethylenediamine) is
View Solution
