A and B are two fixed points 5 cm apart and C is a point on AB such that AC is 3 cm. if the length of AC is increased by 6% the length of CB is decreased by 6% b. 7% c. 8% d. 9%
To solve the problem step by step, we need to analyze the given information and perform the necessary calculations.
Step 1: Identify the initial lengths
We have two fixed points A and B that are 5 cm apart. Point C is located on the line segment AB such that AC = 3 cm. Therefore, we can find the length of CB.
Calculation:
- Length of AB = 5 cm
- Length of AC = 3 cm
- Length of CB = AB - AC = 5 cm - 3 cm = 2 cm
Step 2: Calculate the increase in length of AC
The length of AC is increased by 6%. We need to calculate the new length of AC after this increase.
Calculation:
- Increase in AC = 6% of AC
- Increase = (6/100) * 3 cm = 0.18 cm
- New length of AC = AC + Increase = 3 cm + 0.18 cm = 3.18 cm
Step 3: Calculate the new length of CB
Now, we need to find the new length of CB after the increase in AC.
Calculation:
- New length of CB = AB - New length of AC
- New length of CB = 5 cm - 3.18 cm = 1.82 cm
Step 4: Calculate the decrease in length of CB
Next, we need to determine how much CB has decreased from its original length.
Calculation:
- Original length of CB = 2 cm
- New length of CB = 1.82 cm
- Decrease in length of CB = Original length - New length = 2 cm - 1.82 cm = 0.18 cm
Step 5: Calculate the percentage decrease in length of CB
Finally, we calculate the percentage decrease in the length of CB.
Calculation:
- Percentage decrease = (Decrease / Original length) * 100
- Percentage decrease = (0.18 cm / 2 cm) * 100 = 9%
Conclusion
The length of CB is decreased by 9%. Therefore, the correct answer is option d: 9%.
---
We have two fixed points A and B that are 5 cm apart. Point C is located on the line segment AB such that AC = 3 cm. Therefore, we can find the length of CB.
- Length of AB = 5 cm
- Length of AC = 3 cm
- Length of CB = AB - AC = 5 cm - 3 cm = 2 cm
The length of AC is increased by 6%. We need to calculate the new length of AC after this increase.
- Increase in AC = 6% of AC
- Increase = (6/100) * 3 cm = 0.18 cm
- New length of AC = AC + Increase = 3 cm + 0.18 cm = 3.18 cm
Now, we need to find the new length of CB after the increase in AC.
- New length of CB = AB - New length of AC
- New length of CB = 5 cm - 3.18 cm = 1.82 cm
Next, we need to determine how much CB has decreased from its original length.
- Original length of CB = 2 cm
- New length of CB = 1.82 cm
- Decrease in length of CB = Original length - New length = 2 cm - 1.82 cm = 0.18 cm
Finally, we calculate the percentage decrease in the length of CB.
- Percentage decrease = (Decrease / Original length) * 100
- Percentage decrease = (0.18 cm / 2 cm) * 100 = 9%
The length of CB is decreased by 9%. Therefore, the correct answer is option d: 9%.
Topper's Solved these Questions
Similar Questions
A and B are two fixed points 5 cm apart and C is a point on AB such that AC is 3 cm. if the length of AC is increased by 6% the length of CB is decreased by 6% b. 7% c. 8% d. 9%
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View Solution
Knowledge Check
A and B are two fixed points 5 cm apart and C is a point on AB such that AC in 3 cm. If the length of AC is increased by 6%, the length of CB is decreased by
A0.06B0.07C0.08D0.09In ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
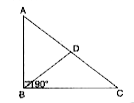 A4 cmB√6 cmC3 cmD3.5 cm
A4 cmB√6 cmC3 cmD3.5 cmIf length of simple pendulum is increased by 6% then percentage change in the time-period will be
A3%B9%C6%D1/9%
If the radius of a circle is increased by 6%, then the area is increased by (a) 6% (b) 12% (c) 12.36% (d) 16.64%
View SolutionAB is a line segment of length 8 cm. Locate a point C on AB such that AC=13CB.
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=6cm. The length of chord BC=
(A) 4.8cm
(B) 9.6cm
(C) 2.4cm
(D) 5cm
View SolutionBy what percent the volume of a cube increases if the length of each edge was increased by 50%? (a) 50% (b) 125% (c) 237.5% (d) 273.5%
View SolutionSum of present ages of P and Q is 41. Age of P 2 year hence is equal to age of R, 1 year ago. Age of P, 4 year hence is equal to age of Q 1 year ago and ratio of present age of P and S is 3 : 4. Find the difference of age of R and S.
View Solution
