As marks in Biology are 20 less than 25% of the total marks obtained by him in Biology, Maths and Drawing. If his marks in Drawing be 50, what are his marks in Maths? 40 b. 45 c. 50 d. cannot be determined
To solve the problem, we need to find the marks in Maths given the conditions about the marks in Biology and Drawing. Let's break it down step by step.
Step 1: Define the Variables
Let:
- B = Marks in Biology
- M = Marks in Maths
- D = Marks in Drawing
From the problem, we know:
- D=50 (marks in Drawing)
- B=25% of total marks obtained in Biology, Maths, and Drawing minus 20.
Step 2: Express Total Marks
Let X be the total marks obtained in Biology, Maths, and Drawing. Thus, we can express the marks in Biology as:
B=0.25X−20
Step 3: Write the Equation for Total Marks
The total marks can be expressed as:
X=B+M+D
Substituting D and B into this equation gives:
X=(0.25X−20)+M+50
Step 4: Simplify the Equation
Now, we can simplify the equation:
X=0.25X−20+M+50
X=0.25X+M+30
Step 5: Rearranging the Equation
Rearranging the equation to isolate M:
X−0.25X=M+30
0.75X=M+30
M=0.75X−30
Step 6: Solve for M
Now, we need to express X in terms of M:
From M=0.75X−30, we can express X as:
0.75X=M+30
X=M+300.75
X=4(M+30)3
Step 7: Substitute Back to Find M
Now, substitute X back into the equation for B:
B=0.25X−20
Substituting for X:
B=0.25(4(M+30)3)−20
B=1(M+30)3−20
B=M+30−603
B=M−303
Step 8: Substitute D into Total Marks Equation
Now substitute B and D back into the total marks equation:
X=B+M+D
X=M−303+M+50
Multiply the entire equation by 3 to eliminate the fraction:
3X=(M−30)+3M+150
3X=4M+120
Now, we can express X in terms of M:
X=4M+1203
Step 9: Set the Two Expressions for X Equal
Now we have two expressions for X:
1. X=4(M+30)3
2. X=4M+1203
Since both expressions are equal, we can set them equal to each other:
4(M+30)3=4M+1203
Step 10: Solve for M
Since the denominators are the same, we can multiply through by 3:
4(M+30)=4M+120
Expanding gives:
4M+120=4M+120
This means that the equations are consistent, but we cannot determine a specific value for M based on the information given.
Conclusion
Since we cannot determine the exact value of M with the information provided, the answer is:
Option D: cannot be determined.
Let:
- B = Marks in Biology
- M = Marks in Maths
- D = Marks in Drawing
- D=50 (marks in Drawing)
- B=25% of total marks obtained in Biology, Maths, and Drawing minus 20.
Let X be the total marks obtained in Biology, Maths, and Drawing. Thus, we can express the marks in Biology as:
B=0.25X−20
The total marks can be expressed as:
X=B+M+D
Substituting D and B into this equation gives:
X=(0.25X−20)+M+50
Now, we can simplify the equation:
X=0.25X−20+M+50
X=0.25X+M+30
Rearranging the equation to isolate M:
X−0.25X=M+30
0.75X=M+30
M=0.75X−30
Now, we need to express X in terms of M:
From M=0.75X−30, we can express X as:
0.75X=M+30
X=M+300.75
X=4(M+30)3
Now, substitute X back into the equation for B:
B=0.25X−20
Substituting for X:
B=0.25(4(M+30)3)−20
B=1(M+30)3−20
B=M+30−603
B=M−303
Now substitute B and D back into the total marks equation:
X=B+M+D
X=M−303+M+50
Multiply the entire equation by 3 to eliminate the fraction:
3X=(M−30)+3M+150
3X=4M+120
Now, we can express X in terms of M:
X=4M+1203
Now we have two expressions for X:
1. X=4(M+30)3
2. X=4M+1203
4(M+30)3=4M+1203
Since the denominators are the same, we can multiply through by 3:
4(M+30)=4M+120
Expanding gives:
4M+120=4M+120
Since we cannot determine the exact value of M with the information provided, the answer is:
Option D: cannot be determined.
Topper's Solved these Questions
Similar Questions
If my marks in maths are less than your markes in Maths by 20% then your marks in Maths are 25% more than my marks in Maths. (True/False)
View SolutionThe total marks obtained by a student in Physics, Chemistry and Mathematics together is 120 more than the marks obtained by him in Chemistry. What is the average marks obtained by him in Physics and Mathematics together? (a) 40 (b) 60 (c) 120 (d) Cannot be determined (e) None of these
View Solution
Knowledge Check
The average of marks obtained by A and B is 15 less than that of average marks obtained by B and C. If the marks obtained by C is 65, what is the marks obtained by A?
A35B50C65D80The average of marks obtained by A and B is 15 less than that of average marks obtained by B and C. If the marks obtained by C is 65, then what is the marks obtained by A?
A35B50C65D80B got 20% marks less than A. What per cent marks did A got more than B?
A20B25C12D80
If my marks in maths are less than your markes in Maths by 20% then your marks in Maths are 25% more than my marks in Maths. (True/False)
View SolutionThe given pie chart shows the marks obtained (in degrees) by a student in different subjects . The total marks obtained by the student in the examination is 432.
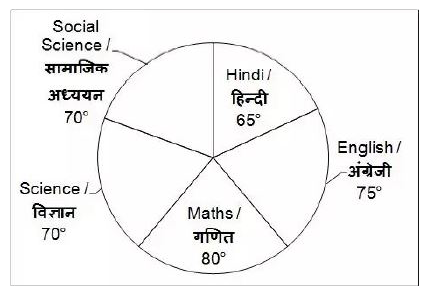
If the maximum marks per subject is 100, then what is the total marks (in percentage) obtained in English and Maths together?
View SolutionIf B got 25% marks less than A, then the marks of A is how much percent more than that of B?
View SolutionThe histogram depicts the marks obtained by 45 students of a class. How many students obtained 50 or more marks and less than 70?
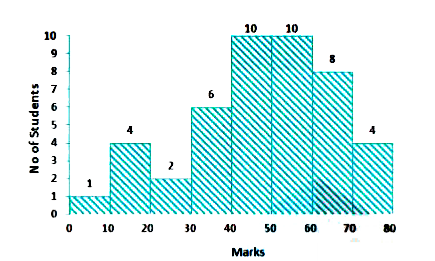
View SolutionA, B and C are three students. A got 36% less marks than B and 16% more marks than C. If B ogt 145 marks , then what are the marks got by C ?
View Solution
