P is a point within or on the circle x2+y2=r2. The probability that the point P is such that it is above the line y=mx is
Step by step video & image solution for P is a point within or on the circle x^2 + y^2 = r^2. The probability that the point P is such that it is above the line y = mx is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If the polar of a point P w.r.t. the circle x2+y2=a2 touches the circle (x−a)2+y2=a2, then P lies on:
View SolutionIf ellipses (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 The tangent lines drawn at P intersect perpendicular to P, then the point p of P x^(2)+y^(2)=a^(2)+b^(2) is. This circle is called
02:07View SolutionThe line y=mx+c intersects the circle x2+y2=r2 in two distinct points if
06:32View SolutionConsider the following figure
find the point of intersection P of the circle
x2+y2=32
and the line y=x
01:09View SolutionConsider the following figure
Find the point of intersection 'P' of the circle
x2+y2=50
and the line y = x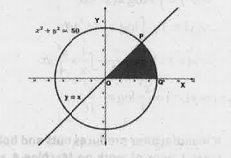
01:55View SolutionIf the line y=mx+c be a tangent to the circle x^2+y^2=a^2 , then the point of contact is
05:22View SolutionThe straight line y=mx+c cuts the circle x2+y2=a2 at real points if
03:44View SolutionThe straight-line y=mx+c cuts the circle x2+y2=a2 in real points if :
03:01View Solution