The values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
[−1,1]
[1,2)
[−1,1]
[-2,-1])
The correct Answer is:B
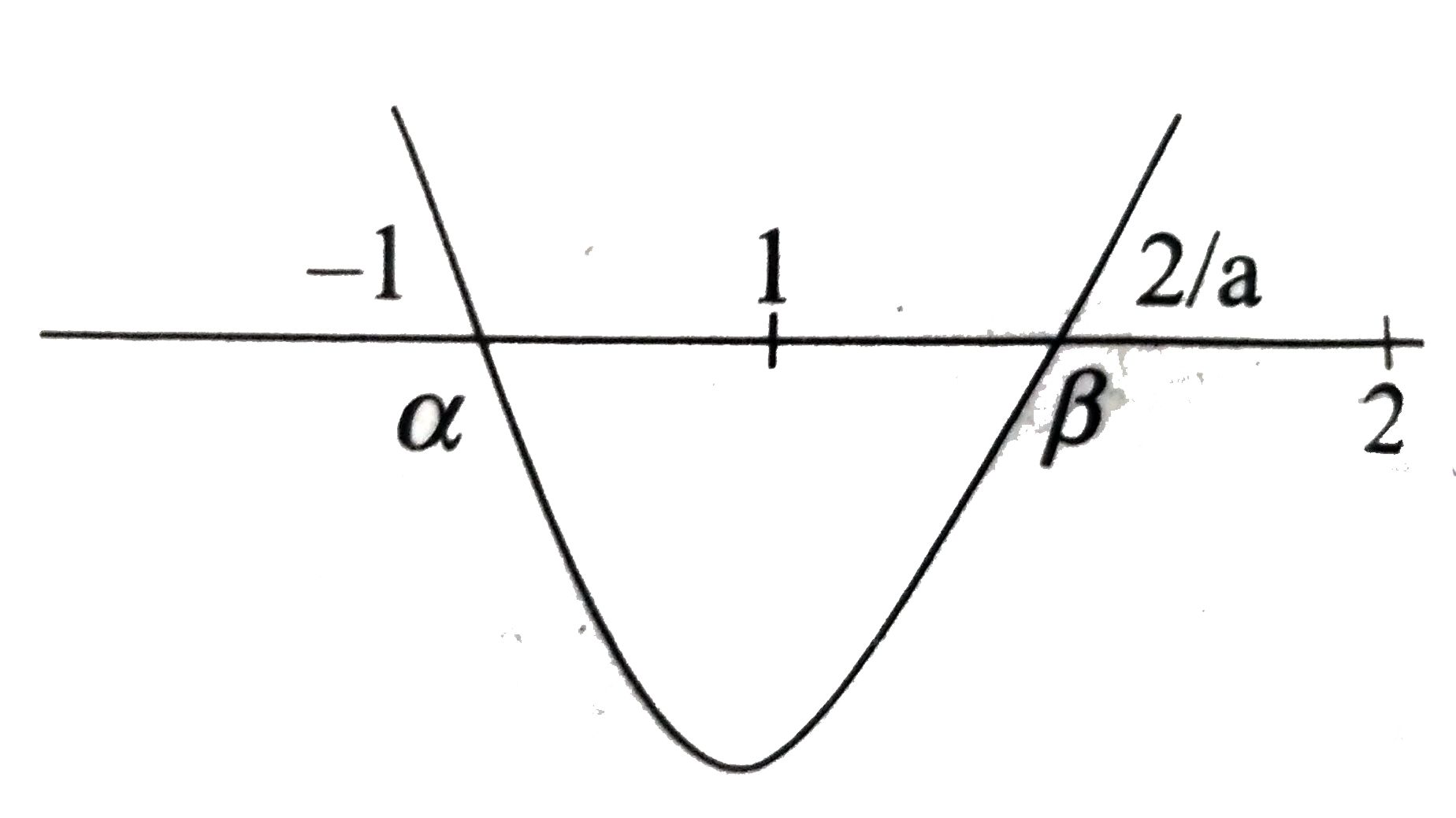
(b) Let f(x)=ax2+(a−2)x−2
f(x) is negative for two integral values of x, so graph should be vertically upward parabola
i.e., a>0
Let two roots of f(x)=0 are α and β, then
α, β=−a(a−2)±(a+2)2a
⇒a=−1, β=2a
⇒1<β≤2
⇒1<2a≤2
⇒a∈[1,2)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension
12 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
Similar Questions
The values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
View SolutionAll the values of 'a' for which the quadratic expression ax2+(a−2)x−2 is negative for exactly two integral values of x may lie in [1,32] (b) [32,2) [1,2) (d) [−1,2)
View Solution
Knowledge Check
The value of 'a' for which the quadratic expression ax2+|2a−3|x−6 is positive for exactly two integral values of x is
A(−34,−35)B(−34,−35]C[−34,−35]D(−34,−710)find the value of x for which the expression 2−3x−4x2 has the greatest value
A−4116B38C−38D4116The set of values of 'a' for which ax2−(4−2a)x−8<0 for exactly three integral values of x, is
A2≤a<4B1≤a<2C2<a<4D1<a<2
The number of integral values of α for which the quadratic expression αx2+|2α−3|x−6 is positive for exactly two integral values of x is equal to
View SolutionThe set of values of 'a' for which f(x)=ax2+2x(1−a)−4 is negative for exactly three integral values of x, is-
View SolutionLargest integral value of 'a' for which the expression y=x2+ax+(a−3) is non positive x∈[0,1] is
View SolutionFor what values of x will the expression x2+2x−8 be negative ?
View SolutionIf the minimum value of the quadratic expression y=ax2+bx+c is negative attained at negative vlaue of x, then :
View Solution
