All complex numbers 'z' which satisfy the relation $| z - | z + 1 | | = | z + | z - 1 ∣ ∣$ on the complex plane lie on the

A

$y = x$

B

$y = - x$

C

circle $x^{2} + y^{2} = 1$

D

line $x = 0$ or on a line segment joining $(- 1, 0) \to$ (1,0)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$(d)$ Given $| z - | z + 1 | |^(2) = | z + | z - 1 ∣ {∣ ∣}^{2}$
$∴ (z - | z + 1 |) (¯ z - | z + 1 |) = (z + | z - 1 |) (¯ z + | z - 1 |)$
$z ¯ z - z | z + 1 | - ¯ z | z + 1 | + {| z + 1 |}^{2}$
$= z ¯ z + z | z - 1 | + ¯ z | z - 1 | + {| z - 1 |}^{2}$
${| z + 1 |}^{2} - {| z - 1 |}^{2} = (z + ¯ z) [| z - 1 | + | z + 1 |]$
$(z + 1) (¯ z + 1) - (z - 1) (¯ z - 1) = (z + ¯ z) [| z - 1 | + | z + 1 |]$
$(z ¯ z + z + ¯ z + 1) - (z ¯ z - z - ¯ z + 1) = (z + ¯ z) [| z - 1 | + | z + 1 |]$
$2 (z + ¯ z) = (z + ¯ z) [| z + 1 | + | z - 1 |]$
$(z + ¯ z) [| z + 1 | + | z - 1 | - 2] = 0$
$\Rightarrow$ Either $z + ¯ z = 0 \Rightarrow z$ is purely imaginary
$\Rightarrow z$ lies on $y$ axis $\Rightarrow x = 0$
or $| z + 1 | + | z - 1 | = 2$
$\Rightarrow z$ lies on the line segment joining $(- 1, 0)$ and $(1, 0)$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The complex numbers z = x + iy which satisfy the equation $∣ ∣ ∣ \frac{z - 5 i}{z + 5 i} ∣ ∣ ∣ = 1$ , lie on

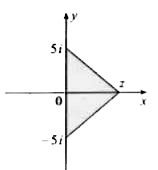Athe x - axis
Bthe straight line y = 5
Ca circle passing through origin
DNone of these
Question 2 - Select One
The complex numbers z = x + iy which satisfy the equation $∣ ∣ ∣ \frac{z - 5 i}{z + 5 i} ∣ ∣ ∣ = 1$ , lie on

Athe x-axis
Bthe straight line y = 5
Ca circle passing through the origin
Dnone of these
Question 3 - Select One or More
The complex number z satisfying the equation $| z - 1 | = | z + 1 | = 1$ is
A0
B1+i
C $- 1 + i$
D $1 - i$

CENGAGE-COMPLEX NUMBERS-Single correct Answer

Home
Ask Doubt
Profile