How many six-digit numbers are there in which no digit is repeated, even digits appear at even places, odd digits appear at odd places and the number is divisible by $4$ ?

A

$3600$

B

$2700$

C

$2160$

D

$1440$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$(d)$ The number formed by last two digits must be divisible by $4$ .

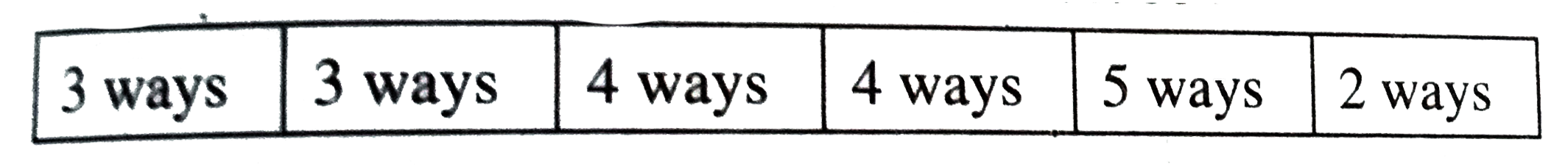
$3 \times 3 \times 4 \times 4 \times 5 \times 2 = 1440$

|

Updated on:21/07/2023

Class 12 MATHS PERMUTATION AND COMBINATION

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Multiple Correct Answer
2videos
PERMUTATION AND COMBINATION
BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8videos
PERMUTATION AND COMBINATION
BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank
21videos
PARABOLA
BOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9videos
PRINCIPLE OF MATHEMATICAL INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
How many 4-digit numbers are there with no digit repeated?
A $= 9 \cdot 9 \cdot 8 \cdot 7$
B $= 10 \cdot 9 \cdot 8 \cdot 7$
C $= 9 \cdot 8 \cdot 7$
DNone of these
Question 2 - Select One
How many three digit numbers are there in which all the digits are odd?
A100
B125
C500
D250
Question 3 - Select One
How many 6-digit numbers have at least 1 even digit?
A884375
B3600
C880775
D15624

CENGAGE-PERMUTATION AND COMBINATION-Question Bank

Home
Ask Doubt
Profile