Three vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they form the vertices of an isosceles triangle is
17
13
37
35
The correct Answer is:D
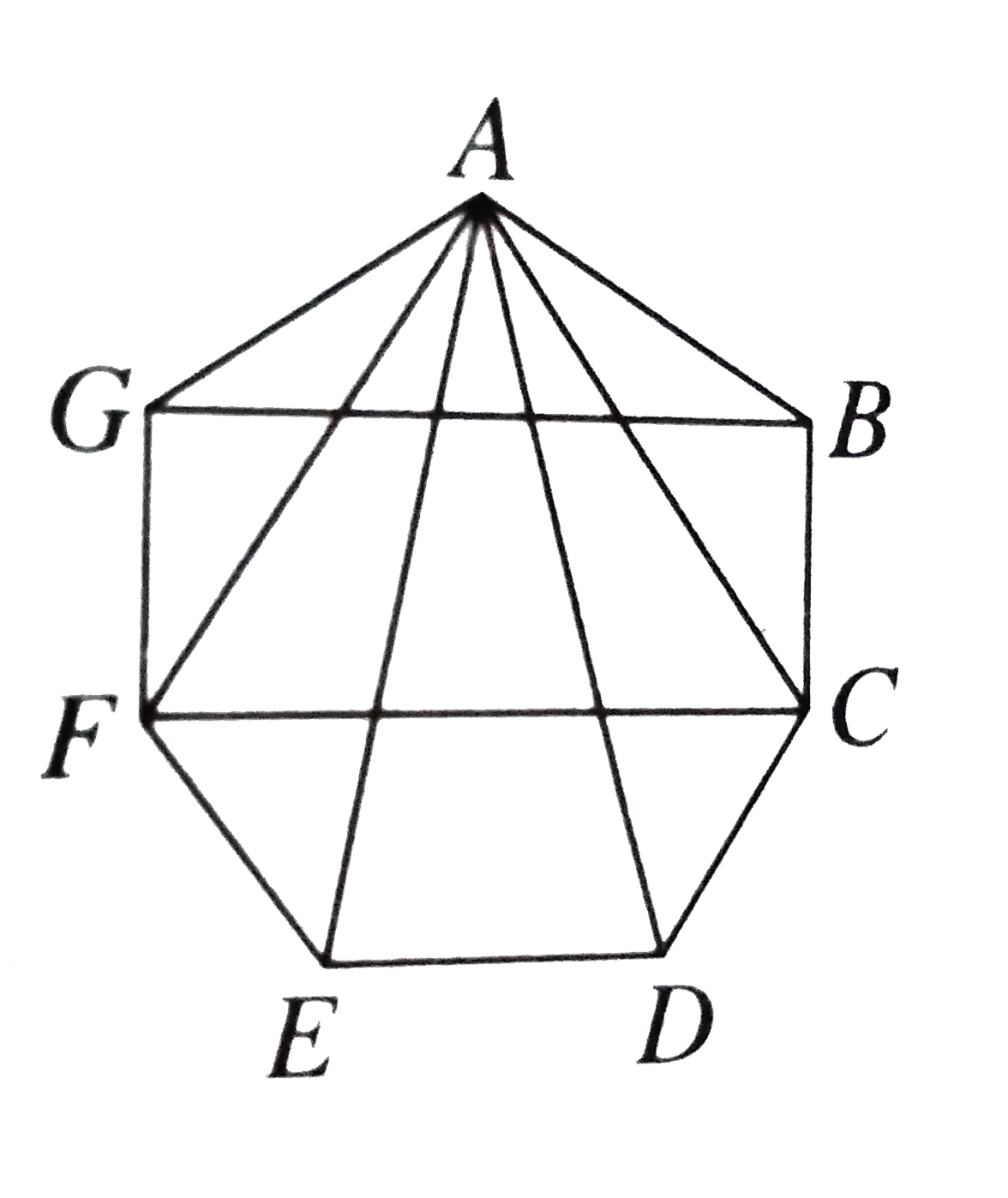
(d) ΔAGB, ΔAFC and ΔAED are isosceles
∴P=7C1×3'7C3=7×37×6×53×2=35
Topper's Solved these Questions
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Multiple Correct Answer
13 Videos
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Comprehension
2 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
Similar Questions
Three distinct vertices are chosen at random from the vertices of a given regular polygon of (2n+1) sides Let all such choices are equally likely and the probability that the centre of the given polygon lies in the interior of the triangle determined by these three chosen random points is 514 Three vertices of the polygon are chosen at random. The probability that these vertices form an isosceles triangle is.
View SolutionThree distinct vertices are randomly chosen among the vertices of a cube. The probability that they from equilateral triangle is
View Solution
Knowledge Check
Three vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they from the vertices of an isosceles triangle is-
A17B13C37D35Three vertices are chosen at random from the vertices of a regular hexagon then the probability that the triangle with these vertices is an equilateral triangle is equal to
A110B35C910D310Three vertices are chosen from the vertices of a regular hexagon, then the probability that they will form an equilateral triangle is
A15B110C215D25
Three of the six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral equals
View SolutionThe number of ways of choosing three vertices fromseven vertices of a regular heptagon such that they form an isosceles triangle, is
View SolutionThree vertices are chosen at random from the vertices of a regular hexagon then
The probability that the triangle has exactly two sides common with the side of the hexagon is
View SolutionThree vertices are chosen at random from the vertices of a regular hexagon then
The probability that the triangle has exactly one side common with the side of the hexagon is
View SolutionThree distinct vertices are randomly selected among the vertices of a cube. The probabiltiy that these vertices form an isosceles or equilateral triangle is
View Solution