The equation of the parabola whose vertex and focus lie on the axis of x at distances a and a1 from the origin, respectively, is y2−4(a1−a)x y2−4(a1−a)(x−a) y2−4(a1−a)(x−a)1) noneofthese
Step by step video & image solution for The equation of the parabola whose vertex and focus lie on the axis of x at distances a and a_1 from the origin, respectively, is y^2-4(a_1-a)x y^2-4(a_1-a)(x-a) y^2-4(a_1-a)(x-a)1) non eoft h e s e by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The equation of the parabola whose vertex and focus lie on the axis of x at distances a and a1 from the origin, respectively, is y2−4(a1−a)x y2−4(a1−a)(x−a) y2−4(a1−a)(x−a)1) noneofthese
View SolutionProve that the equation of the parabola whose vertex and focus lie on x-axis at distances 'a' and 'b' from origin (b>a), is
y2=4(b−a)(x−a).
View Solution
Knowledge Check
The equation of the parabola whose vertex and focus lie on the axis of xat distances aand a1 from the origin respectively, is
Ay2=4(a1−a)xBy2=4(a1−a)(x−a)Cy2=4(a1−a)(x−a1)Dnone of theseThe equation of parabola whose vertex and focus lie on the axis of x at distances a and a1 from the origin respectively, is
Ay2=4(a1−a)xBy2=4(a1−a)(x−a)Cy2=4(a1−a)(x−a1)Dy2=4aa1xThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
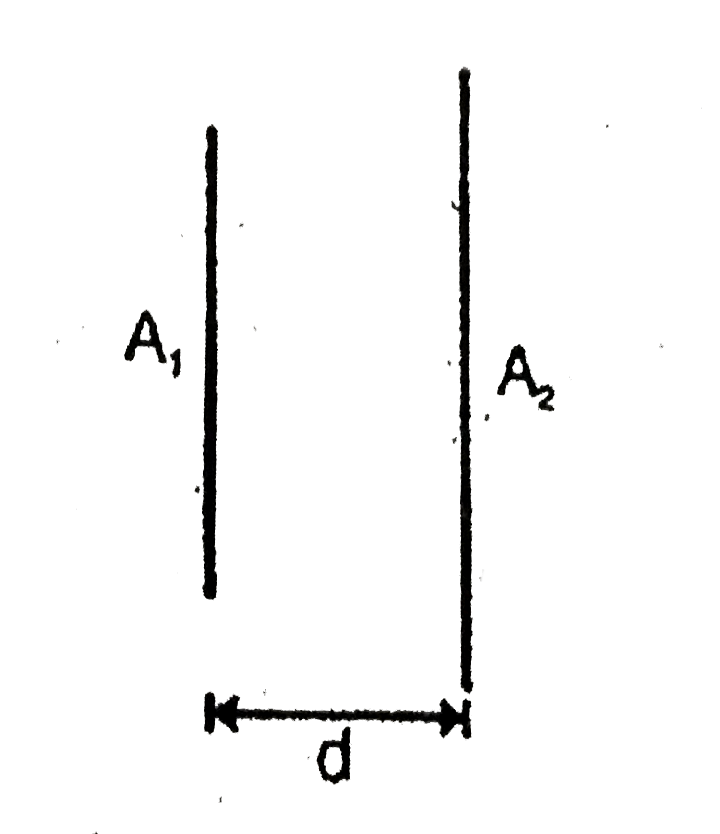 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
The axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (x+y)2=(x−y−2) (x−y)2=(x+y−2) (x−y)2=4(x+y−2) (x−y)2=8(x+y−2)
View SolutionIf distance of vertex and foci from origin are 'a'and'a1' on +x axis of parabola will be y2=4(a1−a)(x−a) such that a1>a.
View SolutionIf the tangent and the normal to x2−y2=4 at a point cut off intercepts a1,a2 on the x-axis respectively & b1,b2 on the y-axis respectively. Then the value of a1a2+b1b2 is equal to:
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
View SolutionWhich of the following species will have the largest and the smallest size Mg,Mg2+,Al,Al3+?
View Solution
