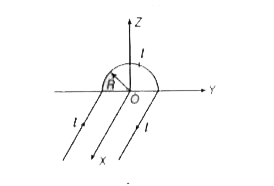
एक तार का आकार यहाँ आरेख में दर्शाया गया है। इससे I धारा प्रवाहित हो रही है। तार के रेखीय भाग बहुत लम्बे हैं और X-अक्ष के समान्तर हैं। तार का अर्द्धवृत्ताकार भाग Y-Z समतल में है और इस भाग की त्रिज्या R है, तो बिन्दु O पर चुम्बकीय क्षेत्र है
B=μ04πlR(πˆi+2ˆk)
B=−μ04πlR(πˆi+2ˆk)
B=−μ0I4πR(2ˆk+πˆi)
B=μ04πlR(πˆi+2ˆk)
The correct Answer is:C
(c) लम्बे रेखीय भाग के कारण एक सिरे पर चुम्बकीय क्षेत्र का सूत्र,
B=μ0i4πd(sin0∘+sin90∘)
d= लम्बवत् दूरी
तथा अर्द्धवृत्ताकार भाग के कारण केन्द्र पर ऐम्पियर के परिपथ नियन से चुम्बकीय क्षेत्र
B=μ0i4Rजहाँ , R=त्रिज्या
[ नोट की दिशा दाए हाथ के अंगूठे के नियम से दी जाती है ]
विभिन्न क्षेत्रों में चुम्बकीय क्षेत्र को निम्न प्रकार से दिया जाता है
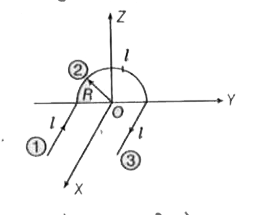
1,2, व 3 तार के कारण चुम्बकीय क्षेत्र
B1=μ04π×lR(−ˆk)(∴d=R)
B3=μ0l4πR(−ˆk)(d=R)
B2=μ0l4R(−ˆi)(r=R)
( यहाँ,l= धारा, R=त्रिज्या, μ0 = निर्वात् की चुम्बकीय पारगम्यता )
केन्द्र O पर कुल चुम्बकीय क्षेत्र,
B=B1+B2+B3
=μ0l4πR(−2ˆk)+μ0l4R(−ˆi)
=−μ0l4πR(2ˆk+πˆi)
Topper's Solved these Questions
Similar Questions
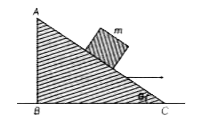
आनत कोण θ के किसी चिकने आनत वेज ARC पर 1 द्रव्यमान का कोई ब्लॉक चित्रानुसार स्थित है। इस वेज को दाईं ओर कोई त्वरण दिया जाता है। ब्लॉक को वेज पर स्थिर रखने के लिए a औरθ के बीच सम्बन्ध होगा
 02:48View Solution
02:48View Solutionदो आवेशित कण किसी एकसमान चुम्बकीय क्षेत्र B=B0ˆk में पूर्णतः सर्वसम सर्पिल पथो पर विपरीत दिशाओ में गमन करते है तो इनके
05:14View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
04:32View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
02:29View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
02:24View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionx-अक्ष के समान्तर समतल का समीकरण है
07:31View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता हैView SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
View Solutionनिम्नांकित में से कौन-सा निबंध का एक भाग है?
02:20View Solutionनिम्नांकित में से कौन-सा.निबंध का एक भाग है,?
02:09View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
05:43View Solutionएक 713 मीटर लम्बे तार को 7 बराबर भागों में काटा जाता है तब प्रत्येक भाग की लम्बाई होगी
View SolutionA solid sphere of brass with a radius 15 cm is drawn into a wire of diameter 6 mm. The length of the wire ( in cm ) is :
15 cm त्रिज्या वाले पीतल के एक ठोस गोले को 6 mm व्यास के तार में खिंचा जाता है | तार की लम्बाई (cm में) है:View Solutionएक ठोस का निर्माण होता है और इसमें तीन प्रकार के परमाणु X, Y और Z होते हैं। X एक fcc जालक बनाता है, जिसमें Y परमाणु सभी चतुष्फलकीय रिक्तियों पर अधिविन्यासित होते हैं और Z परमाणु अष्टफलकीय रिक्तियों के आधे भाग पर अधिविन्यासित होते हैं। ठोस का सूत्र है
View Solutionतत्वों O, S, Se और As में परमाणु त्रिज्या के बढ़ते आकार का क्रम है:
01:15View Solution

