Question

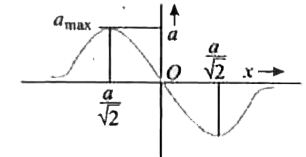
y- अक्ष पर मूल बिंदु O से समान दूरियों पर दो सदृश धनात्मक आवेशों को अवस्थित किया गया है। x- अक्ष के साथ गमन करता हुआ मूल बिंदु O से गुजरते हुए इससे अति दूर निकल जाता है। इसके त्वरण को इसकी गति की दिशा में धनात्मक माना जाता है , तो कण के त्वरण और इसके x-निर्देशांक के मध्य ग्राफ को किसके द्वारा सर्वोत्तम रूप से व्यक्त किया गया है ?

Options

A.
B.
C.
D.

Answer

c

Explanation

माना कि दो समान धनात्मक आवेश (+q) मूल बिन्दु O के दोनों ओर, मूल बिन्दु से दूरी a पर रखे हैं तथा एक ऋणात्मक आवेश (-q.) बिन्दु O से बहुत अधिक दूरी x पर रखा है।

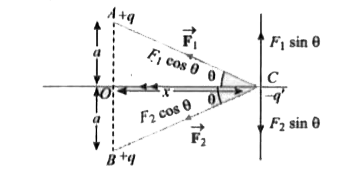
यहाँ `F_(1)=F_(2)=k=(qq.)/((a^(2)+x^(2)))" "...(i)`
`AC=BC= sqrt(a^(2)+x^(2))` और `cos theta=(x)/(sqrt(a^(2)+x^(2))`
स्थिति चित्र के अनुसार दिखाई गयी है। यहाँ ऊर्ध्वाधर घटक `F_(1)sin theta` और `F_(2)sin theta` बराबर और विपरीत हैं अत: ये एक-दूसरे को निरस्त कर देंगे।
और आवेश . पर परिणामी बल
`rArr F=F_(1) cos theta+F_(2) cos theta`
`rArr F=2F cos theta" " [ :. F_(1)=F_(2)]`
`rArr F=2k(qq.x)/((a^(2)+x^(2))^(3//2))" "...(ii)`
लेकिन F = ma यहाँ m=आवेश. का द्रव्यमान, a = त्वरण
अब `ma=2k(qq.x)/((a^(2)+x^(2))^(3//2))`
`rArr a=(2kqq.)/(m)*(x)/((a^(2)+x^(2))^(3//2))" "...(iii)`
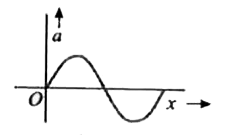
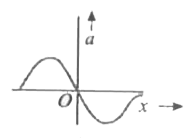
जब कण चलना प्रारम्भ करता है तो उसका त्वरण शून्य है और उसके बाद कण का त्वरण समी (iii) से दिया जाता है। इसलिए यह स्पष्ट है कि जब x = 0, तब a= 0 और जब `x=+-(a)/(sqrt(2))` तव कण का त्वरण अधिकतम है। अत: त्वरण और x निर्देशांक के बीच ग्राफ इस प्रकार दिया जाता है।