द्रव्यमान M तथा त्रिज्या R वाले एक ठोस गोले में R2 त्रिज्या का एक गोलीय कोटर इस प्रकार स्थित है कि कोटर का केन्द्र गोले के केन्द्र से R/2 दूरी पर है। एक बिन्दु संहति कोटर के अन्दर गोले के केन्द्र से R/4 दूरी पर स्थित है। गोले तथा बिन्दु संहति के मध्य गुरुत्वीय खिंचाव का मान होगा
11GM/R2
14GMm/R2
GM/2R2
GMm/R2
The correct Answer is:B
बिन्दु द्रव्यमान m पर खिंचाव बल की गणना के लिए हम इस पर ठोस गोले से लगने वाले बल की गणना करते हैं तथा इस बल को जो बल खोखले गोले पर लगता है में से घटाते हैं अर्थात्
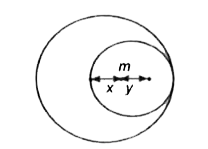
F=GmM(x)2−GmM.y2 [x=R/4,x+y=R/2]
M=(43)πR3ρ and M.=43π(R2)3ρ=M8
F=GMn(R/4)2−Gm(M/8)(R/4)2
=14GmMR2
Topper's Solved these Questions
Similar Questions
[ML2T−3] विमायें व्यक्त करता है।
View Solutionएक आयताकार साबुन की फिल्म का आकार 8 सेमी ×3.75 सेमी से बढ़ाकर 10 सेमी ×6 सेमी करने में किया गया कार्य 2×10−4 जूल है। इस साधुन की फिल्म का पृष्ठ तनाव (न्यूटन मीटर) में होगा
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (ˆi+2ˆj−3ˆk) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं ( 1,0,0), ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्र समतल 3x−y+z=2पर स्थित है।
View Solutionयदि गोले का संदिश समीकरण r^(2) - vec( r ) . ( 8vec( i ) - 6 vec( j ) + 10 vec( k )) - 50 = 0 है तो गोले का केंद्र और त्रिज्या ज्ञात कीजिए।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं (1,0,0) , ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्रे समतल x - y + z = 2 पर स्थित है।
View Solution
