From the curve y=|x| , draw (i)y=|x−1|+1 (ii)y=|x+1|−1 (iii)y=|x+2|+3Solution in Tamil
Step by step video & image solution for From the curve y= |x| , draw (i) y= |x-1| + 1 """" (ii) y= |x+1|-1 """ (iii) y=|x+2|+3 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that sin4x+sin2xcos4x+cos2x=tan3x.
View SolutionThe total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m,
C(m) = 0.4 m + 50 and S(m) = 0.03 m . Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
View SolutionThe relation R defined on a set A = { 0,-1,1,2} by xRy if |x2+y2∣≤2 , then which one of the following is true?
View SolutionIf tanA-tanB=x and cotB-cotA=y , then cot(A-B) . is equal to (i) 1/y-1/x (ii) 1/x-1/y (iii)1/y+1/x (iv) 1/(x+y)
View SolutionDraw the graph of followings (i) y=-|x + 2| (ii) y=||x-1|-2| (iii) y = |x + 2| + |x - 3| (iv) |y| + x = -1
View SolutionDraw the following curves: (i)y=||x^(2)|-2x-3| (ii) |x|+|y|=1 (iii) |y|=|log|x||( iv )y=sqrt(2-x^(2))
View SolutionDraw the graphs of
(i) y=x2(x−1)|x−2|
(ii) y=x3(x−1)|x−2|
View SolutionIf graph of y=(x−1)(x−2) is

then draw the graph of the following
(i)y=|(x−1)(x−2)| (ii)|y|=(x−1)(x−2)
(iii)y=(|x|−1)(|x|−2) (iv)|(|x|−1)(|x|−2)|
(v)|y|=|(|x|−1)(|x|−2)|
View Solutionx-y relation is given by y=xn calculate the value of n in the following :-
(i)y=x2x2/3
(ii)y=x3/2x1
(iii)y=x1/2x1/2
(iv)y=x3/2√x
View SolutionDraw the graph of polynominal funtions
(i)y=x+1(ii)y=x2(iii)y=x3+1(iv)y=x(x−1)(x−2)
View SolutionFrom the curve y=x, draw
y=x+1
View SolutionFrom the curve y=x, draw
y=12x+1
View SolutionFrom the curve y= |x|, draw
y = |x-1|+1
View SolutionFrom the curve y= |x|, draw
y= |x+1|-1
View Solutionகொடுக்கப்பட்டுள்ள படத்தில்y=x3 என்ற வளை வரியின் படத்தினை பயன்படுத்தி அச்சு மதிப்பு மாறாமல் ஒரே தளத்தில் கீழ்காணும் சார்புகளை வரைக(i) y=−x3 (ii)y=x3+1 (iii)y=x3−1 (iv)y=(x+1)3
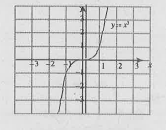
View Solution
