In a class, the number of students who like only Chess, only Caroms, both the games and neither of the games are in the ratio 2:4:1:3. the number of students who like at least one of these games is 120 more than those who like neither of the games. Find the number of students in the class.
300
240
270
360
The correct Answer is:A
Let the number of students who like only Chess be 2x. The number of students who like only Carroms. Both the games and neither of the gains are 4x,x and 3x respectively.
Given, 2x+4x+x=3x+120
⇒4x=120⇒x=30
∴ The total number of students =2x+4x+x+3x=10x=300.
Topper's Solved these Questions
- SETS AND RELATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SETS AND RELATIONSEXERCISE - LEVEL 2
24 Videos
- SALES TAX AND COST OF LIVING INDEX BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SALES TAX AND COST OF LIVING INDEX EXERCISE - Level 3
14 Videos
- SHARES AND DIVIDENDSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SHARES AND DIVIDENDSEXERCISE - CONCEPT APPLICATION (LEVEL 3)
10 Videos
Similar Questions
In a locality the number of residents who read only the hindu, only the Times of India. Both the newspaers and neither of the newspapers are in the ratio 2:3:4:1 The number of residents who read at least one of these newspapers is 160 more than those who read neither of these newspapers. find the number of residents in the locality.
View SolutionIn the following Venn diagram the total number of students who play all the three games is:
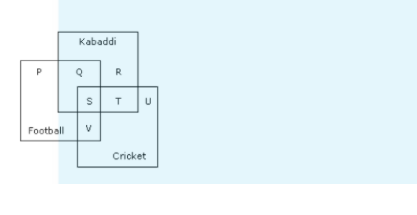
View Solution
Knowledge Check
The students of a class like at least one of the games out of Chess, Caroms and Judo. The number of students who like only Chess and Caroms, only Caroms and Judo, only Chess and Judo and the number of those who like all the three are equal. The number of students who like only Chess, only Caroms, only Judo and the number of those who like all the three are equal. A possible value of the number of students in the class is
A30B40C50D70A class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
A34B32C38D36A class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
A34B32C38D36
In a class of 50 students 32 likes Mathematics , 24 like Science and 12 like both . Find the number of students who like neither of the two subjects.
View SolutionIn a group of 36 students, 18 like volleyball, 12 like hockey, and 14 like neither of the games. How many like both games?
View SolutionIn a class ,there are 80 students ,The ratio of the number of those who like only chocolates only ice creams ,both of these ,and neither of these is 4:3:2:1.How many like utmost one of the chocolates and ice creams ?
View SolutionIn a class ,there are 80 students ,The ratio of the number of those who like only chocolates only ice creams ,both of these ,and neither of these is 4:3:2:1.How many like utmost one of the chocolates and ice creams ?
View SolutionIn a school 80 students like chocolate, 40 like coffee if the number of students doesn't like any of them is equal to the number of students who like both of them then what is the total number of students in the school?
View Solution
