Question

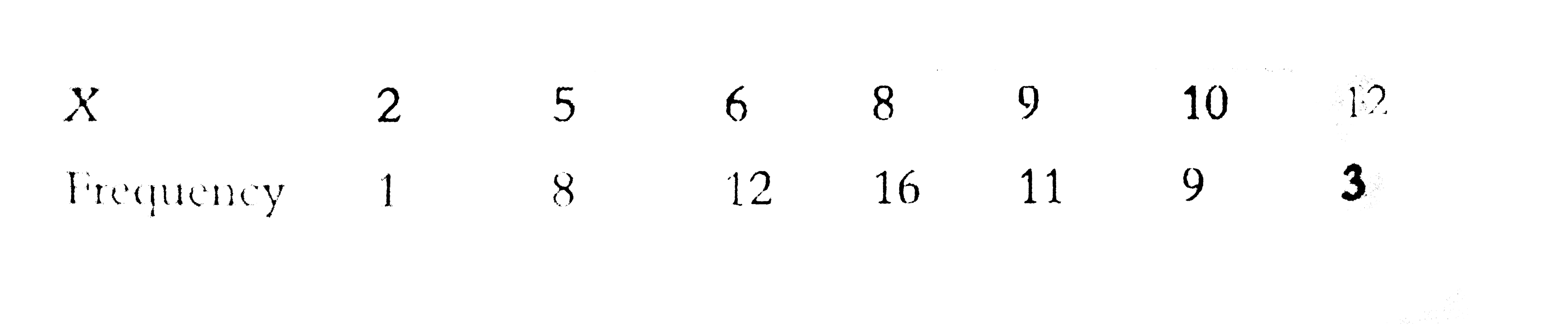
The semi-inter quartile range of the observations 9, 12, 14, 6, 23, 36, 20, 7, 42 and 32 is

Options

A. 12.75
B. 12.5
C. 11.5
D. 9.5

Answer

C

Explanation

To find the semi-interquartile range (also known as the quartile deviation) of the given observations, we will follow these steps:

Step 1: Arrange the Data in Ascending Order
First, we need to arrange the given observations in ascending order.

Given Observations: 9, 12, 14, 6, 23, 36, 20, 7, 42, 32

Arranged in Ascending Order: 6, 7, 9, 12, 14, 20, 23, 32, 36, 42

Step 2: Find the Quartiles
To find the semi-interquartile range, we need to calculate the first quartile (Q1) and the third quartile (Q3).

Total number of observations (n) = 10

Q1 Calculation:
- The first quartile (Q1) is the median of the first half of the data.
- The first half of the data (first 5 observations): 6, 7, 9, 12, 14
- The median of these 5 numbers is the third number (since there are 5 numbers): Q1 = 9

Q3 Calculation:
- The third quartile (Q3) is the median of the second half of the data.
- The second half of the data (last 5 observations): 20, 23, 32, 36, 42
- The median of these 5 numbers is the third number: Q3 = 32

Step 3: Calculate the Semi-Interquartile Range
Now, we can use the formula for the semi-interquartile range:

\( \text{Semi-Interquartile Range} = \frac{Q3 - Q1}{2} \)

Substituting the values we found:

\( \text{Semi-Interquartile Range} = \frac{32 - 9}{2} = \frac{23}{2} = 11.5 \)

Final Answer
The semi-interquartile range of the observations is 11.5.

---