If pq=rs=tu then p2+r2+t2q2+s2+u2=
prtqsu
1
p3+r3+t3q3+s3+u3
(p+r+tq+s+u)2
The correct Answer is:D
To solve the problem, we start with the given condition:
pq=rs=tu
Let's denote this common ratio as λ. Thus, we can express p, r, and t in terms of q, s, and u:
1. Express p, r, and t in terms of λ:
p=λq
r=λs
t=λu
2. Substitute p, r, and t into the expression:
We need to find the value of:
p2+r2+t2q2+s2+u2
Substituting the values of p, r, and t:
=(λq)2+(λs)2+(λu)2q2+s2+u2
3. Simplify the numerator:
The numerator becomes:
=λ2q2+λ2s2+λ2u2q2+s2+u2
4. Factor out λ2:
We can factor out λ2 from the numerator:
=λ2(q2+s2+u2)q2+s2+u2
5. Cancel out the common terms:
Since q2+s2+u2 appears in both the numerator and the denominator, we can cancel them out:
=λ2
Thus, the final result is:
p2+r2+t2q2+s2+u2=λ2
p=λq
r=λs
t=λu
We need to find the value of:
p2+r2+t2q2+s2+u2
Substituting the values of p, r, and t:
=(λq)2+(λs)2+(λu)2q2+s2+u2
The numerator becomes:
=λ2q2+λ2s2+λ2u2q2+s2+u2
We can factor out λ2 from the numerator:
=λ2(q2+s2+u2)q2+s2+u2
Since q2+s2+u2 appears in both the numerator and the denominator, we can cancel them out:
=λ2
p2+r2+t2q2+s2+u2=λ2
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - LEVEL 219videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - LEVEL 36videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - Essay Type Question5videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PROFIT AND LOSS DISCOUNT AND PARTNERSHIP EXERCISE - CONCEPT APPLICATION (LEVEL 2)29videos
PROFIT AND LOSS DISCOUNT AND PARTNERSHIP
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - REAL NUMBERS AND LCM AND HCF EXERCISE - level -111videos
REAL NUMBERS AND LCM AND HCF
Similar Questions
If →P+→Q=→R and →P−→Q=→S, then R2+S2 is equal to
(A) P2+Q2
(B) 2(P2−Q2)
(C) 2(P2+Q2)
(D) 4PQView SolutionIn Fig.88 PR is a straight line and ∠PQS:∠SQR=7:5. The measure of ∠SQR is (a) (b)(c)(d)(e)60(f)0(g)(h)(i) (j) (b) (k)(l)62(m)(n)(o)1p2(q)(r)(s)0(t)(u)(v) (w) (c) (d)(e)67(f)(g)(h)1i2(j)(k)(l)0(m)(n)(o) (p) (d) (q)(r)(s)(t)75(u)0(v)(w)(x) (y)
View Solution
Knowledge Check
- Question 1 - Select One
Find the value of p2+q2r2+s2 , if p:q=r:s
A14B19CpqrsD(p−qr−s)2 - Question 2 - Select One
Find the value if p2+q2r2+s2 if p:q::r:s
A14BpqrsC(p+qr+s)2Dboth b and c - Question 3 - Select One
If x(x−1)(x2+1)2=Px−1+Qx+Rx2+1+Sx+T(x2+1)2, then P+Q−R−S+T=____________.
A54B32C97D89
If p,q,r are in A.P the p2(q+r),q2(r+p),r2(p+q) are in
View SolutionIn the given quadrilateral ABCD , p∘+q∘=1002, a∘=140∘ and r∘=12(a2+q∘). Find the angles p∘,q∘,r∘ and s∘.
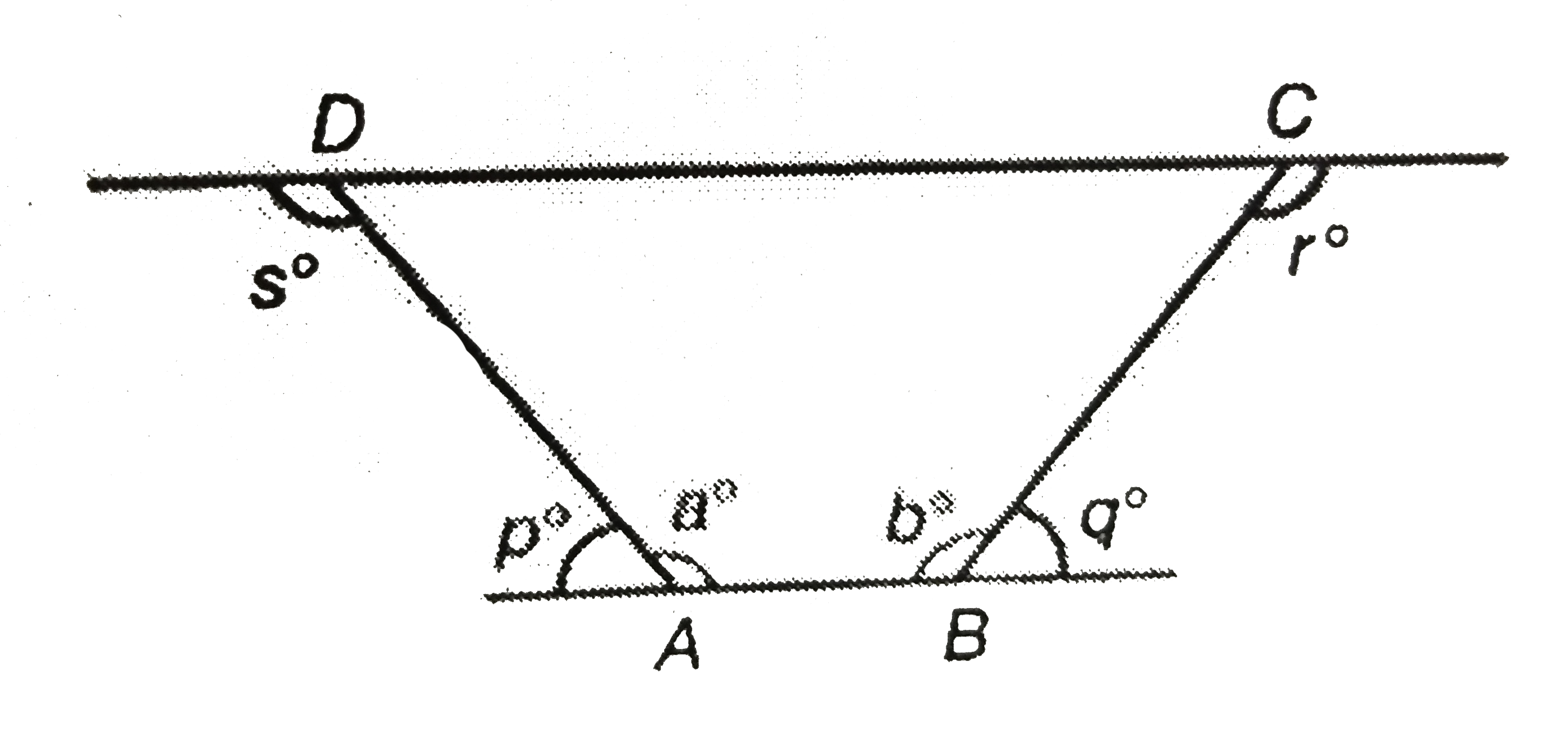 View Solution
View Solution.prove that (ap+q)2(aq+r)2(ar+p)2(ap⋅aq⋅ar)4=1
View SolutionIn an A.P., SpSq=p2q2,p≠q, then T6T21 is equal to
View SolutionIn an A.P., SpSq=p2q2,p≠q, then T6T21 is equal to
View Solution

