In the given circle of radius R,find the speed and velocity in each case if the time taken
(a) to travel from A to B is 11s
(b) to complete the circle is 22 s
To solve the problem, we need to calculate the speed and velocity for two different scenarios involving a circle of radius R.
Given:
- Radius of the circle = R
- Time taken from A to B = 11 seconds
- Time taken to complete the circle = 22 seconds
(a) To travel from A to B in 11 seconds:
1. Calculate the distance from A to B:
- The distance from A to B is half the circumference of the circle.
- Circumference of the circle = 2πR
- Therefore, distance from A to B = 2πR2=πR
2. Calculate the speed:
- Speed is defined as distance traveled divided by the time taken.
- Speed = DistanceTime=πR11
3. Calculate the displacement:
- The displacement is the straight-line distance from point A to point B.
- Since A and B are points on the circumference of the circle, the displacement is equal to the chord length between A and B. For simplicity, we assume A and B are directly opposite each other, which gives us a displacement of 2R.
4. Calculate the velocity:
- Velocity is defined as displacement divided by the time taken.
- Velocity = DisplacementTime=2R11
Summary for (a):
- Speed = πR11
- Velocity = 2R11
---
(b) To complete the circle in 22 seconds:
1. Calculate the distance traveled:
- The distance traveled when completing the circle is the full circumference.
- Circumference = 2πR
2. Calculate the speed:
- Speed = DistanceTime=2πR22=πR11
3. Calculate the displacement:
- Since the particle returns to the starting point A after completing the circle, the displacement is 0 (the initial and final positions are the same).
4. Calculate the velocity:
- Velocity = DisplacementTime=022=0
Summary for (b):
- Speed = πR11
- Velocity = 0
---
- Radius of the circle = R
- Time taken from A to B = 11 seconds
- Time taken to complete the circle = 22 seconds
- The distance from A to B is half the circumference of the circle.
- Circumference of the circle = 2πR
- Therefore, distance from A to B = 2πR2=πR
- Speed is defined as distance traveled divided by the time taken.
- Speed = DistanceTime=πR11
- The displacement is the straight-line distance from point A to point B.
- Since A and B are points on the circumference of the circle, the displacement is equal to the chord length between A and B. For simplicity, we assume A and B are directly opposite each other, which gives us a displacement of 2R.
- Velocity is defined as displacement divided by the time taken.
- Velocity = DisplacementTime=2R11
- Speed = πR11
- Velocity = 2R11
- The distance traveled when completing the circle is the full circumference.
- Circumference = 2πR
- Speed = DistanceTime=2πR22=πR11
- Since the particle returns to the starting point A after completing the circle, the displacement is 0 (the initial and final positions are the same).
- Velocity = DisplacementTime=022=0
- Speed = πR11
- Velocity = 0
Topper's Solved these Questions
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - ESSAY TYPE QUESTIONS
3 Videos
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - LEVEL 1
45 Videos
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS)
30 Videos
- CHEMICAL EFFECTS OF ELECTRIC CURRENTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - CHEMICAL EFFECTS OF ELECTRIC CURRENTEXERCISE - COMPETITION CORNER (MCQ)
48 Videos
Similar Questions
A car is going round a circle of radius R1 with constant speed. Another car is going round a circle of radius R2 with constant speed.If both of them take same time to complete the circles,the ratio of their angular speeds and linear speeds will be
View SolutionA pencil is tied to one end of a string of length 5 cm and the other is fixed to a nail. If the time taken to draw a half circle and a full circle, with the pencil is 2 and 4 seconds, respectively, find the speed and velocity pecil
(a) to draw half circle is drawn.
(b) when full circle is drawn
View Solution
Knowledge Check
A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
A500radsB150radsC50radsD15radsA car is going round a circle of radius R1 with constant speed. Another car is going round a circle of radius R2 with constant speed. If both of them take same time to complete the circles, the ratio of their angular speeds and linear speeds will be
A√R1R2,R1R2B1,1C1, R1R2DR1R2 , 1An electron is moving in a circle of radius 2m with speed 4 m/s . Find the acceleration of the electron
A8m/s2B4m/s2C16m/s2D10m/s2
A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
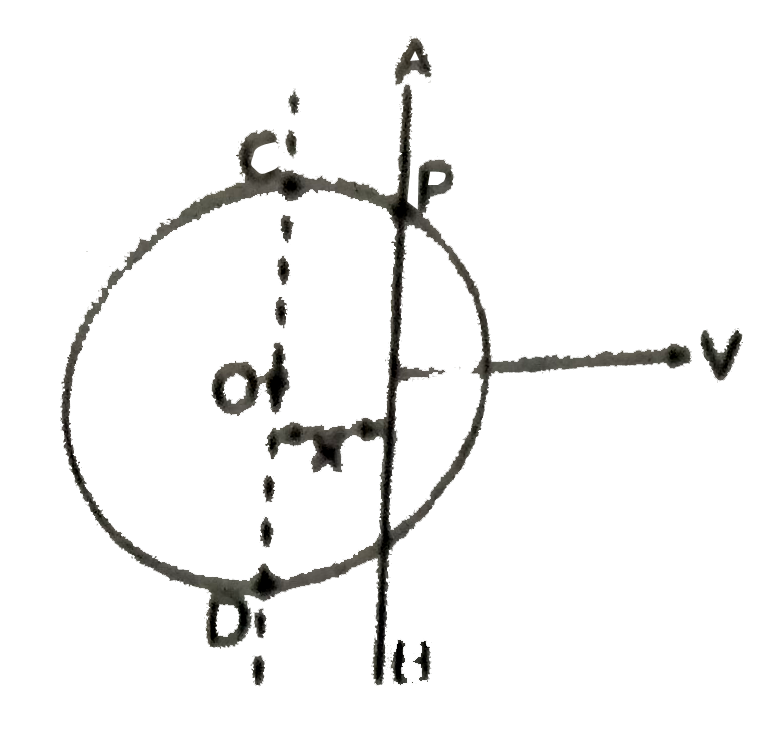
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View SolutionA particel comes round a circle of radius 1 m once. The time taken by it its 10s. The average velocity of motion is
View SolutionAn athelete runs alongs a circular track of radius 14 m with a speed of 11 m s−1 then the time taken by the althete to complete 6 rounds is ______
View SolutionA particle travels two and a half revolutions of the circle of radius R in time t. The ratio of the average speed of the particle to the magnitude of the average velocity in this time interval is
View SolutionA particle is moving in a circle of radius 4cm with constant speed of 1cm/s. Find
(a) time period of the particle.
(b) average speed, average velocity and average acceleration in a time interval from t=0 to t=T4. Here, T is the time period of the particle. Give only their magnitudes.
View Solution
