A car of mass 1000 kg is moving with a certain speed when a constant braking force 1000 N acts on it for 5s and the speed of the car reduces to half its original speed. Find the further time required to stop the car if the same constant force acts.
To solve the problem, we will follow these steps:
Step 1: Calculate the acceleration (deceleration) due to the braking force.
The formula for acceleration is given by:
a=Fm
Where:
- F is the braking force (1000 N)
- m is the mass of the car (1000 kg)
Substituting the values:
a=1000N1000kg=1m/s2
Since this is a braking force, the acceleration will be negative (deceleration):
a=−1m/s2
Step 2: Determine the initial speed of the car.
Let the initial speed of the car be u. After applying the braking force for 5 seconds, the speed reduces to half of its original speed. Therefore, the final speed v after 5 seconds is:
v=u2
Using the equation of motion:
v=u+at
Substituting the known values:
u2=u−1×5
u2=u−5
Step 3: Solve for the initial speed u.
Rearranging the equation:
u2−u=−5
−u2=−5
Multiplying both sides by -2:
u=10m/s
Step 4: Calculate the time required to stop the car from its current speed.
Now that we know the initial speed u=10m/s, we can find the time t required to stop the car using the same braking force (deceleration):
Using the equation:
v=u+at
Where the final speed v=0:
0=10−1×t
Step 5: Solve for t.
Rearranging the equation:
t=10seconds
Step 6: Calculate the total time required to stop the car.
The total time required to stop the car is the time during which the braking force was applied (5 seconds) plus the time calculated to come to a complete stop (10 seconds):
Total time=5seconds+10seconds=15seconds
Step 7: Find the further time required to stop the car after the initial 5 seconds.
The further time required to stop the car after the initial 5 seconds is:
Further time=10seconds
Thus, the final answer is:
The further time required to stop the car is 10 seconds.
The formula for acceleration is given by:
a=Fm
Where:
- F is the braking force (1000 N)
- m is the mass of the car (1000 kg)
a=1000N1000kg=1m/s2
a=−1m/s2
Let the initial speed of the car be u. After applying the braking force for 5 seconds, the speed reduces to half of its original speed. Therefore, the final speed v after 5 seconds is:
v=u2
v=u+at
Substituting the known values:
u2=u−1×5
u2=u−5
Rearranging the equation:
u2−u=−5
−u2=−5
Multiplying both sides by -2:
u=10m/s
Now that we know the initial speed u=10m/s, we can find the time t required to stop the car using the same braking force (deceleration):
Using the equation:
v=u+at
Where the final speed v=0:
0=10−1×t
Rearranging the equation:
t=10seconds
The total time required to stop the car is the time during which the braking force was applied (5 seconds) plus the time calculated to come to a complete stop (10 seconds):
Total time=5seconds+10seconds=15seconds
The further time required to stop the car after the initial 5 seconds is:
Further time=10seconds
The further time required to stop the car is 10 seconds.
Topper's Solved these Questions
- DYNAMICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - DYNAMICSEXERCISE - Level 3
14 Videos
- DYNAMICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - DYNAMICSEXERCISE - EXAMPLE
11 Videos
- DYNAMICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - DYNAMICSEXERCISE - Level 1
45 Videos
- CHEMICAL EFFECTS OF ELECTRIC CURRENTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - CHEMICAL EFFECTS OF ELECTRIC CURRENTEXERCISE - COMPETITION CORNER (MCQ)
48 Videos
- ELECTRICITYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - ELECTRICITYEXERCISE - CONCEPT APPLICATION (Level 3)
10 Videos
Similar Questions
A Car of mass 1000 kg is moving with a velocity of 10m/s under the action of a forward force of 1000N and retarding force of 500 N due to friction. Wath be its velocity after 5 seconds ?
View SolutionA car of mass 1000 kg moving with a speed of 30m/s collides with the back of a stationery lorry of mass 9000 kg. Calculate the speed of the vehichles immediately after the collision if they remain jammed together.
View Solution
Knowledge Check
A car moving with a velocity v is stopped within a distance x by applying a retarding force F. If the speed of the car is doubled, then the force required to stop the car with the same distance is
A2FB3FC4FDF/4A car of mass 1000 kg negotiates a banked curve of radius 90 m on a frictionless road. If the banking angle is 45∘, the speed of the car is
A20ms−1B30ms−1C5ms−1D10ms−1A car of mass =m=1000kg is moving with constant speed v=100m/s on a parabolic shaped bridge AFOE of span force applied by the bridge on the car when he car is at point E, is:
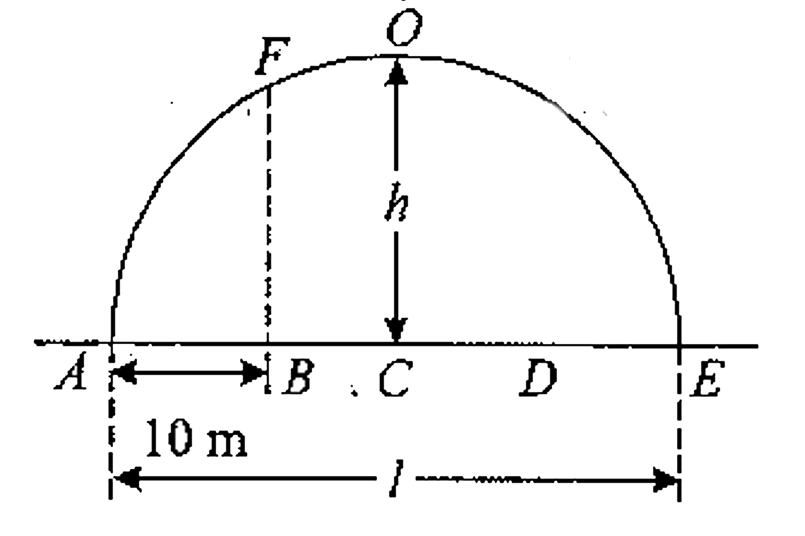 A5000√52NB5000√2NC10000√2ND5000√25N
A5000√52NB5000√2NC10000√2ND5000√25N
2A car of 1000 kg moving with a velocity of 18km/hr is stopped by the brake force of 1000 N. The distance covered by it before coming to rest is -
View SolutionA car of mass 2400 kg moving with a velocity of 20 m s−1 is stopped in 10 seconds on applying brakes Calculate the retardation and the retarding force.
View SolutionA car moving with a constant speed on a straight track takes a band in a curve with the same speed. Due to this
View SolutionA car of mass 1000kg negotiates a banked curve of radius 90m on a fictionless road. If the banking angle is 45∘ the speed of the car is:
View SolutionA car of mass m = 1000 kg is moving with constant speed v = 10 m/s on a parabolic shaped bridge AFOE of span l=40m and height h = 20 m as shown in the figure. Then the net force applied by the bridge on the car when the car is at point F, is

View Solution
