An object of weight is lifted by using a hydraulic press. The radii of the cross sections of the pump piston and press piston are 10 cm and 20 cm, respectively. Calculate the effort required to lift the object. Calculate the displacement of the load if the effort is moved through a distance of 20 cm.
To solve the problem, we need to calculate the effort required to lift an object using a hydraulic press and the displacement of the load when the effort is moved through a certain distance.
Step 1: Calculate the Weight of the Object
First, we need to calculate the weight of the object in Newtons. The weight is given as 500 kg (wt). To convert this to Newtons, we use the formula:
Weight (W)=mass (m)×g
where g (acceleration due to gravity) is approximately 9.8m/s2.
W=500kg×9.8m/s2=4900N
Step 2: Calculate the Areas of the Pistons
Next, we calculate the areas of the pump piston and the press piston.
- Radius of the pump piston r1=10cm=0.1m
- Radius of the press piston r2=20cm=0.2m
The area A of a circle is given by:
A=πr2
Calculating the areas:
A1=π(0.1)2=π(0.01)≈0.0314m2
A2=π(0.2)2=π(0.04)≈0.1256m2
Step 3: Apply the Hydraulic Principle
According to Pascal’s principle, the pressure applied on the smaller piston is equal to the pressure on the larger piston:
F1A1=F2A2
Where:
- F1 is the effort (force applied on the pump piston)
- F2 is the load (weight of the object)
Rearranging the equation gives:
F1=F2⋅A1A2
Substituting the known values:
F1=4900N⋅0.03140.1256
Calculating F1:
F1=4900N⋅0.25=1225N
Step 4: Calculate the Displacement of the Load
Next, we need to calculate the displacement of the load when the effort is moved through a distance of 20 cm (0.2 m).
Using the principle of conservation of volume:
A1⋅h1=A2⋅h2
Where:
- h1 is the displacement of the effort (0.2 m)
- h2 is the displacement of the load
Rearranging gives:
h2=A1⋅h1A2
Substituting the known values:
h2=0.0314⋅0.20.1256
Calculating h2:
h2=0.006280.1256≈0.05m=5cm
Final Results
- The effort required to lift the object is approximately 1225 N.
- The displacement of the load when the effort is moved through a distance of 20 cm is 5 cm.
First, we need to calculate the weight of the object in Newtons. The weight is given as 500 kg (wt). To convert this to Newtons, we use the formula:
Next, we calculate the areas of the pump piston and the press piston.
- Radius of the press piston r2=20cm=0.2m
According to Pascal’s principle, the pressure applied on the smaller piston is equal to the pressure on the larger piston:
- F1 is the effort (force applied on the pump piston)
- F2 is the load (weight of the object)
Next, we need to calculate the displacement of the load when the effort is moved through a distance of 20 cm (0.2 m).
- h1 is the displacement of the effort (0.2 m)
- h2 is the displacement of the load
- The effort required to lift the object is approximately 1225 N.
- The displacement of the load when the effort is moved through a distance of 20 cm is 5 cm.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - Level 310videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS)43videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - Level 145videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HEATEXERCISE - CONCEPT APPLICATION Level 310videos
HEAT
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICS EXERCISE - CONCEPT APPLICATION (Level 3) (Application Based Questions )5videos
KINEMATICS
Similar Questions
The cross-section of two piston in hydraulic press are 2cm2and150cm2 respectivley . Calculate the minimum force required to support a weight of 2000kg wt on the broader face of the press.
View SolutionIn a hydraulic press, the area of smaller and larger pistons are 5cm2and20cm2, respectively. Calculate the weight which can be raised by larger piston if a force of 100 kgf is applied on smaller piston.
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass 100 kg is to be lifted by a 10 kg effort. The possible values of the area of cross sections of the pump piston and press piston are ____ and ____, repectively, both in the same unit.
A100, 1B10,1C1100D2, 20 - Question 2 - Select One
An object of mass 100 kg is to be lifted by a 10 kg effort. The possible values of the area of cross sections of the pump piston and press piston are ____ and ____, repectively, both in the same unit.
A100, 1B10, 1C1, 100D2, 20
2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
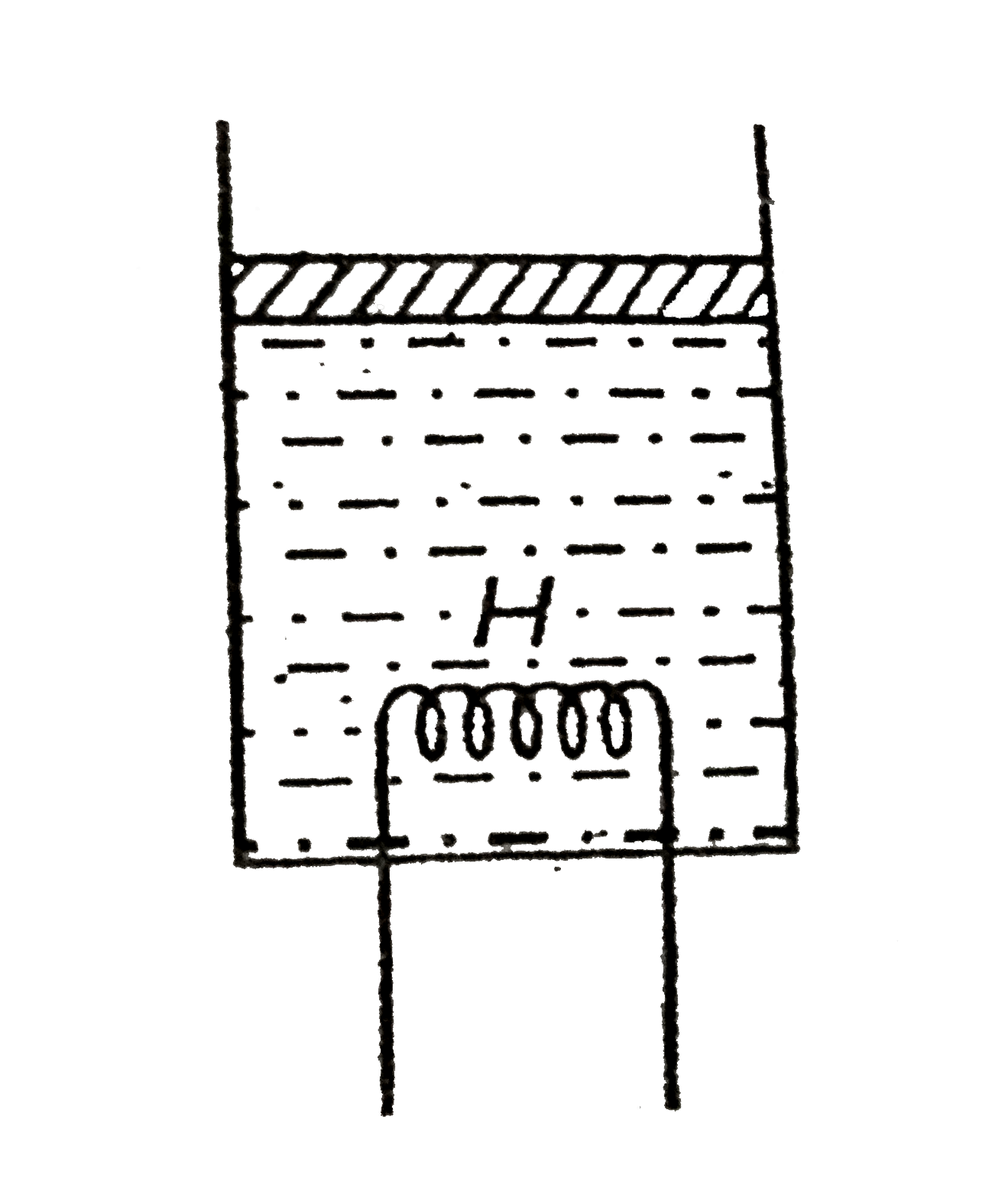 .View Solution
.View SolutionIn a hydraulic press used for lifting heavy loads, the diameters of smaller and larger pistons are 2 cm and 5 cm, respectively. If the smaller piston is pushed in through 5 cm, then by how much distance will the larger piston move out?
View SolutionThe diameters of smaller and larger pistons in a hydraulic press are 3 cm and 15 cm respectively. To move out the larger piston by 0.4 cm calculate the distance through which the smaller piston should be pushed in.
View SolutionIn an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
View SolutionAn object is 60 cm in front of a thin lens, the image being 300 cm on the other side of the lens. Calculate the displacement of the image, when the object is moves 20 cm nearer to the lens.
View SolutionThe following figure shows the use of a lever.
(i) Give an example of this class of lever and
(ii) if FA= 10 cm, AB= 510 cm, calculate the minimum effort required to lift the load.
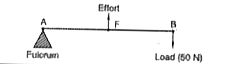 View Solution
View Solution

