Find the ratio of time periods of two pendula whose lengths are in the ratio 1:4
T1T2=√l1l2=√14=12⇒T1:T2=1:2
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVE MOTION AND SOUNDEXERCISE - level 315videos
WAVE MOTION AND SOUND
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVE MOTION AND SOUNDEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS )19videos
WAVE MOTION AND SOUND
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVE MOTION AND SOUNDEXERCISE - Level 145videos
WAVE MOTION AND SOUND
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - STARS AND THE SOLAR SYSTEMEXERCISE - COMPETITION CORNER37videos
STARS AND THE SOLAR SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the ratio of circumferences of two circles, whose areas are in the ratio of 16 : 25.
A16:25B4:5C5:4D25:16 - Question 2 - Select One
Find the ratio of circumference of two circles whose areas are in the ratio of 16:25.
A16:25B4:5C5:4D25:16 - Question 3 - Select One
The time period of a spring - mass system is T. If this spring is cut into two parts, whose lengths are in the ratio 1:2, and the same mass is attached to the longer part, the new time period will be
A√13TB√23TC√3T2D√3T
Find the ratio of lengths of two pendula whose time periods are in the ratio 1:4
View SolutionFind the ratio of lengths of two pendula whose time periods are in the ratio 1:4
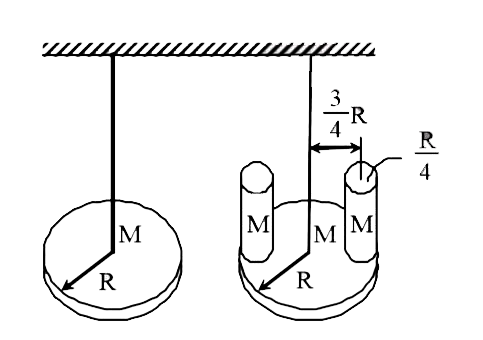
View SolutionFind the ratio of the periods of the two torsion pendula shown in figure. The two differ only by the addition of cylindrical masses as shown in the figure. The radius of each additional mass is 1/4 the radius of the disc. Each cylinder and disc have equal mass.
 View Solution
View SolutionTime period of a spring mass system is T.If this spring is cut into two parts whose lengths are in ratio 1:3 and the same mass is attached to the longer part, the new time period will be
View SolutionA spring of force constant k is cut into two pieces whose lengths are in the ratio 1:2. The force constant of the longer piece?
View Solution

