(b) (i) Calculate the magnetic moment of $T i^{3 +}$ and $V^{4 +}$
(ii) Draw all possible isomers of the complex ${[C o {(e n)}_{2} C l_{2}]}_{2}^{+}$ and identify the optically active isomer.

Text Solution

Verified by Experts

(b) (i) $T i (Z = 22) T i^{3 +} 3 d^{1}$
$V (Z = 23) V^{4 +} 3 d^{1}$
$∴ μ = \sqrt{1 (1 + 2)} = \sqrt{3} = 1.73 μ_{B}$ . So they are paramagnetic
(ii) 1. Cis $[C o {(e n)}_{2} C l_{2}]$

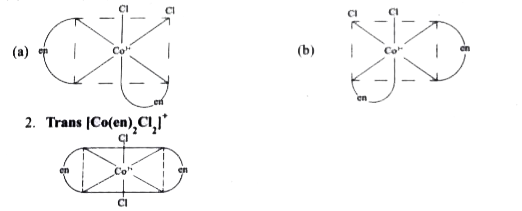
${[C o {(e n)}_{2} C l_{2}]}_{2}^{+}$
The coordination complex ${[C o {(e n)}_{2} C l_{2}]}_{2}^{+}$ has three isomers two optically active cis forms and the optically inactive trans form.

Updated on:21/07/2023

The possible geometric isomers of the complex , ${[C o (e n) B r_{2} C l_{2}]}_{2}^{-}$ is :
A2
B3
C4
D6
Number of possible isomer for the complex $[C o {(e n)}_{2} C I_{2}] C I$ will be: (em = ethylenediamine)
A3
B4
C2
D1
The total No. of isomers possible for the complex $[C o {(e n)}_{2} C l_{2}]$ is :-
A2
B3
C4
D5