Explain about the geometrical isomerism of octahedral complexes with suitable example.

Text Solution

Verified by Experts

$(i)$ Octahedral complexes of the type ${[M A_{2} B_{4}]}^{n \pm}$ , ${[M {(x x)}_{2} B_{2}]}^{n \pm}$ shows cis-trans isomerism. Hence A and B are monodentate ligands and $x x$ is bidentate ligand with two same kind of donor atoms. In the octahedral complex, the position of ligands is indicated by the following numbering scheme.

$(i i)$ The positions $(1, 2) (1, 3) (1, 4) (1, 5), (2, 3) (2, 5) (2, 6), (3, 4) (3, 6), (4, 5) (4, 6)$ and $(5, 6)$ are identical and if two similar groups are present in any one of these positions, the isomer is referred as a cis-isomer.
$(i i i)$ Similarly positions $(1, 6), (2, 4)$ and $(3, 5)$ are identical and if similar groups (or) ligands are present in these positions it is referred as a trans-isomer.
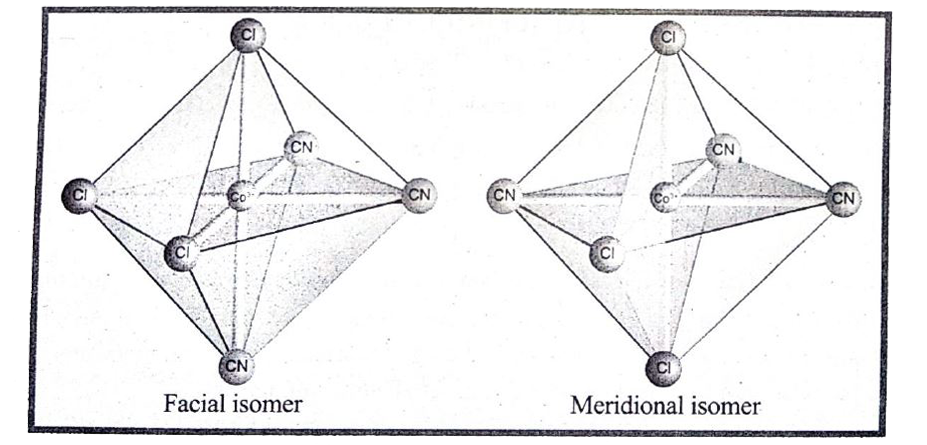
$(i v)$ Octahedral complex of the type ${[M A_{3} B_{3}]}^{n \pm}$ also shows geometrical isomerism. If the three similar ligands (A) are present in the corners of one triangular face of the octahedron and the other $3$ ligands (B) are present in the opposite triangular face, then the isomer is referred as a facial isomer (fac isomer).
$(v)$ If the three similar ligands are present around the meridian which is an imaginary semicircle from one apex of the octahedral to the opposite apex, the isomer is called a meridional isomer (mer is omer). This is called a meridional because each set of ligands can be regarded as lying on a meridian of an octahedran.

Updated on:21/07/2023