Question

एम्पीयर के नियम का उपयोग करते हुए अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र का व्यंजक प्राप्त कीजिए।

Explanation

ऐम्पियर के नियम से अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र नीचे दिये गये चित्र में किसी अनन्त लम्बाई अर्थात् अत्यधिक लम्बाई का सीधा चालक तार है जिसमें I धारा प्रवाहित हो रही है।

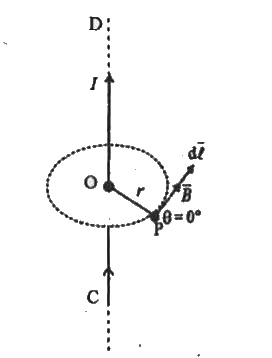
इससे r दूरी पर एक बिन्दु P स्थित है जिस पर हमें चुम्बकीय क्षेत्र के मान की गणना करनी है तार की लम्बाई, दूरी r के सापेक्ष अत्यधिक होने से तार को अनन्त लम्बाई का माना जा सकता है। इसके लिए हम r त्रिज्या का वृत्त, तार के चारों ओर खींचते हैं और बिन्दु P पर एक लम्बाई के अल्पांश की हम कल्पना करते हैं।
चित्र से स्पष्ट है कि चुम्बकीय क्षेत्र `vecB` की दिशा तथा अल्पांश `vec(dl)` की दिशा एक ही है।
ऐम्पियर के नियम से
`intvecB.vec(dl)=mu_0sumi`
यहाँ पर `mu_0` निर्वात या वायु के लिए पारगम्यता गुणांक है।
`intB.dlcos theta =mu_0I " " because sumi=I`
यहाँ पर `vecB` तथा `vec(dl)` एक ही दिशा में है।
अत: `theta = 0°^@` लेने पर
`rArr intB.dlcos 0^@=mu_0I`
`rArr intB.dl=mu_0I`
`B intdl=mu_0I`
`Bxx2pir=mu_0I " " [because intdl="परिधि" =2pir]`
`B=(mu_0I)/(2pir)`..(1)
इस चुम्बकीय क्षेत्र की दिशा को दक्षिण हस्त नियम से ज्ञात करते हैं।
स्पष्ट है कि अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र `vecB` का परिमाण
(i) प्रवाहित धारा I के समानुपाती होता है।
`B prop I`
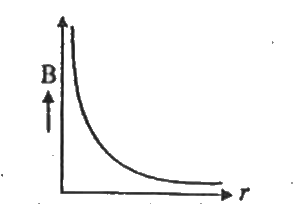
(ii) चालक से लम्बवत् दूरी r के व्युत्क्रमानुपाती होता है। अर्थात् `vecB` में दूरी के साथ परिवर्तन को चित्र में दर्शाया गया है।