किसी रेखीय प्रोग्रमन समस्या के लिए सम्भाव्य क्षेत्र हमेशा रैखिक बहुभुज होता है |
The correct Answer is:असत्य
Topper's Solved these Questions
- बोर्ड प्रश्न-पत्र 2019BOOK - YUGBODHCHAPTER - बोर्ड प्रश्न-पत्र 2019EXERCISE - प्रत्येक का एक शब्द/वाक्य में उत्तर दीजिए-
5 Videos
- बोर्ड प्रश्न-पत्र 2019BOOK - YUGBODHCHAPTER - बोर्ड प्रश्न-पत्र 2019EXERCISE - खण्ड - "ब"
41 Videos
- बोर्ड प्रश्न-पत्र 2019BOOK - YUGBODHCHAPTER - बोर्ड प्रश्न-पत्र 2019EXERCISE - रिक्त स्थानों की पूर्ति कीजिए-
5 Videos
- प्रायिकता BOOK - YUGBODHCHAPTER - प्रायिकता EXERCISE - दीर्घ उत्तरीय प्रश्न-II
31 Videos
- रैखिक प्रोग्रामन BOOK - YUGBODHCHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्न
8 Videos
Similar Questions
x1/x का महत्तम मान है |
View Solutionयदि A=[2432] तथा A=[1325], तो A.B का मान ज्ञात कीजिए |
View Solutionसदिश 3ˆi−2ˆj+6ˆk की दिककोज्याये …………………. हैं |
View Solutionरायपुर में 20% व्यक्ति अंग्रेजी का अखबार पड़ते है, 40% व्यक्ति हिंदी तथा 5% व्यक्ति दोनों प्रकार के अखबार पड़ते है। कितने प्रतिशत व्यक्ति कोई भी अखबार नहीं पड़ते है?
View Solution(B)असमीकरण 3x+2y≤6का ग्राफ खींचिए।
View Solutionबताइए कि दिए हुए कथन सत्य हैं या असत्य
किसीLPPकासुसंगतक्षेत्रसदैवएक.....बहुभुजहोताहै∣∣
View Solutionनिचे दिए गए कथन सत्य है या असत्य ?
किसी रेखीय प्रोग्रामन समस्या के लिए संभाव्य क्षेत्र हमेशा रैखिक बहुभुज होता है।
View Solutionसुसंगत क्षेत्र होता है
View Solutionसुसंगत क्षेत्र के बाहा भाग के किसी भी बिंदु को कहते है
View Solutionनिम्न प्रमेय को समझाइए।
प्रमेय 1. यदि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा उद्देश्य फलन Z=ax+by है। जब Z के एक इष्टतम मान ( अधिकतम या न्यूनतम ) हो जहाँ व्यवरोधों से सम्बंधिर चर और y रैखिक समीकरणों द्वारा व्यक्त हों तब इस इष्टतम मान सुसंगत क्षेत्र के कोनों (शीर्षों )पर होता है।
View Solutionनिम्न प्रमेय को समझाइए।
प्रमेय 2. यदि किसी रैखिक समस्या के लिए सुसंगत क्षेत्र R प्रतिबद्ध हो, तो उद्देश्य फलन के सुसंगत क्षेत्र R में अधिकतम तथा न्यूनतम मान दोनों होते हैं। ये मान सुसंगत क्षेत्र के कोनीय बिंदुओं पर होते हैं।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं -
रैखिक प्रोग्रामन का सुसंगत क्षेत्र ज्ञात करके इसके कोनीय बिंदुओं (शीर्ष बिंदुओं ) को ज्ञात करते हैं।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि किसी रेखीय प्रोग्रामन समस्या के दो अनुकूलतम हल हैं, तो फिर उसके अनंत अनुकूलतम हल होंगे।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
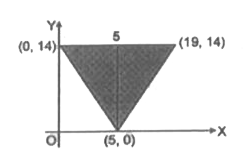
View Solutionरेखीय प्रक्रमन समस्या z=2x+y जबकि 5x+10y≤50,x+y≥1,y≤4 तथा x,y≥0 के लिए z का न्यूनतम मान है
View Solution
