D,E और F क्रमश: त्रिभुज ABC की भुजाओं BC,CAऔर AB के मध्य – बिंदु है। दर्शाइए कि :
(i) BDEF एक समांतर चतुर्भुज है
(ii) ar (DEF)=14ar(ABC)
(ii)ar(BDEF)=12ar(ABC)
Step by step video & image solution for D,E और F क्रमश: त्रिभुज ABC की भुजाओं BC,CAऔर AB के मध्य – बिंदु है। दर्शाइए कि : (i) BDEF एक समांतर चतुर्भुज है (ii) ar (DEF ) = (1)/(4) ar (ABC ) (ii) ar (BDEF ) = (1)/(2) ar (ABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल EXERCISE - पाठय-पुस्तक (प्रश्नावली) (9.4)
4 Videos
- समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल EXERCISE - अभ्यास के लिए प्रश्न (अति लघु उत्तरात्मक प्रश्न )
2 Videos
- समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर चतुर्भुजो और त्रिभुजों के क्षेत्र फल EXERCISE - पाठय-पुस्तक (प्रश्नावली) (9.2)
5 Videos
- संख्या पद्धति BOOK - MBD HINDI-HARYANA BOARDCHAPTER - संख्या पद्धति EXERCISE - बहुविकल्पी प्रश्न
22 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफलBOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफलEXERCISE - अभ्यास के लिए प्रश्न
3 Videos
Similar Questions
समांतर चतुर्भुंज ABCD और आयत ABEF एक ही आधार AB पर स्थित है। और उनके क्षेत्र फल बराबर है। दर्शाइए। कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
View Solution∣∣gmABCD में AB=14cm भुजाओं AB और AD संगत शीर्ष लम्बव8cm और 7cm है। AD ज्ञात कीजिए।
View Solutionयदि E,F,G और H क्रमश: समांतर चतुर्भुज ABCD की भुजाओं के मध्य – बिंदु है तो दर्शाइए कि
ar(EFGH)=12ar(ABCD) है।
View Solutionपरिमेय संख्या 340 बराबर है |
View Solution||gmABCD में, AB=14cm भुजाओं AB और AD के संगत शीर्षलम्ब 8 cm और 7 cm है | AD ज्ञात कीजिए |
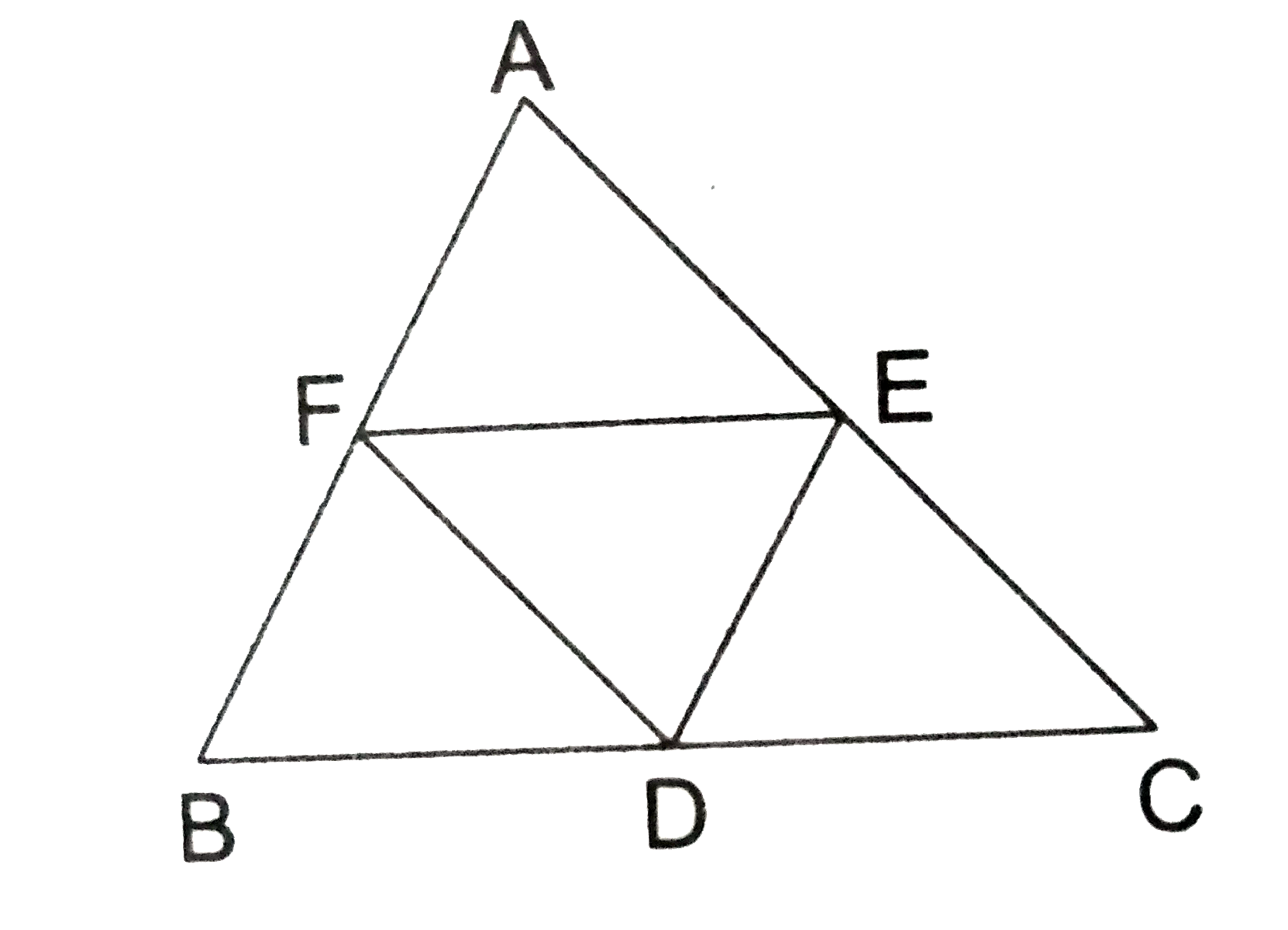
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है |दर्शाइए
(i)ar(PQR)=12ar(ARC)
(ii)ar(RQC)=38ar(ABC)
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
View SolutionD, E तथा F, ΔABC कि क्रमश : भुजाओ BC, CA तथा AB के मध्यबिंदु है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ΔABC के क्षेत्रफल का आधा है।
यह भी दिखाइए कि ar(DEF)=14ar(ABC).
View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
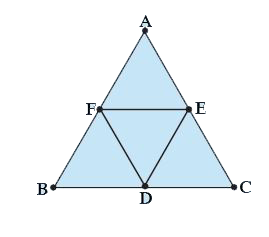
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
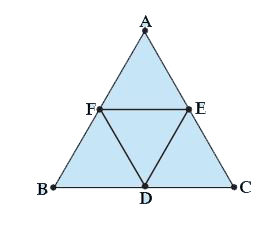
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
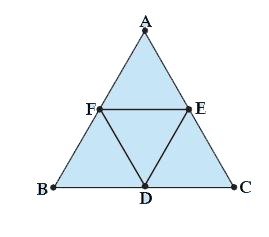
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View Solution
