उस A.P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22वाँ पद 149 है।
The correct Answer is:अतः, दी गई A.P. के प्रथम 22 पदों का योग 1661 है।
Step by step video, text & image solution for उस A.P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22वाँ पद 149 है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर श्रेढ़ीEXERCISE - प्रश्नावली(5.4)5videos
समांतर श्रेढ़ी
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर श्रेढ़ीEXERCISE - अभ्यास के लिए प्रश्न95videos
समांतर श्रेढ़ी
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर श्रेढ़ीEXERCISE - प्रश्नावली(5.2)20videos
समांतर श्रेढ़ी
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - संख्यिकीEXERCISE - दीर्घ उत्तरात्मक प्रश्न1videos
संख्यिकी
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - समांतर श्रेढ़ीEXERCISE - लघु उत्तरात्मक प्रश्न15videos
समांतर श्रेढ़ी
Similar Questions
A.P. : 121, 117, 113, ... का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
04:28View Solutionनिम्नलिखित में से कौन-कौन-सी A.P. हैं ? यदि कोई A.P. हैं, तो इसका सार्व अंतर ज्ञात कीजिए।
(i) 3, 6, 12, 24, .......
(ii) 0, -4.- 8, - 12....... 1 1 1 1
(iii)12,14,(1)/(6),(1)/(6),(1)/(2)<br>(iv)12,2,−8,−18,.........<br>(1)3,3,3,3........__(vi)p.p+90,p+180,p+270,......<br>जहांp= (999)^(999)(vii)1.0,1.7,2.4,3.1......(viii)−225,−425,−625,−825..........(ix)10,10+2^(5),10 + 2^(6),10+2^(7)........
(x) a+b, (a + 1) + b. (a + 1) + (b+ 1),(a + 2) + (b+ 1), (a + 2) + (b + 2).....06:25View Solutionनिम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a , सार्व अंतर d और nवाँ पद a_nहै:
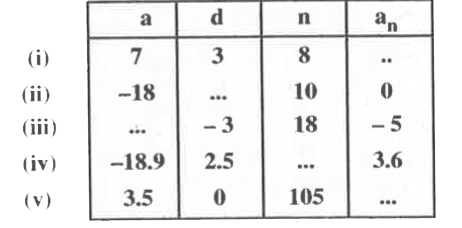03:31View Solutionनिम्नलिखित आंकड़े का माधयक 52.5 है । x और y के मान ज्ञात करे यदि कुल बारम्बारता 100 है ।
06:54View Solutionऐसे प्रथम 40 घन पूर्णांकों का योग ज्ञात कीजिए, जो 6 से विभाज्य हो |
03:48View Solutionउन श्रेढियों के n पदों तक योगफल ज्ञात कीजिए जिनके n वे पद निम्नलिखित है -
n3−3n2+2n04:38View Solutionश्रेढी 2×4+4×6+6×8+….. का 20 वां पद और 20 पदों का योगफल ज्ञात कीजिए ।
07:52View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
03:53View Solution(1−x)−4 के प्रसार में व्यापक पद ज्ञात कीजिए और तब प्रसार के पहले पांच पदों को लिखिय |
09:16View Solution(1+2x)5/2 का प्रथम ऋणात्मक पद ज्ञात कीजिए|
08:20View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
02:14View Solutionएक समान्तर श्रेढ़ी में पदों की संख्या सम ( even ) है| उसके विषम पदों का योग 24 तथा सम पदों का योग 30 है और अंतिम पद, प्रथम पद से 1012 अधिक है | पसं की संख्या एवं श्रेढ़ी ज्ञात कीजिए |
04:18View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
03:49View Solutionनिम्नलिखित श्रेणियों का n पदों तक योग ज्ञात कीजिए ।
1+32+54+78+…............02:23View Solutionउस त्रिभुज का अतः केंद्र ज्ञात कीजिए जिसके शीर्षों के निर्देशांक (1,2),(2,3) और (3,1) है ।
04:16View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (3,-4) से होकर जाती है और अक्षों से बराबर परन्तु विपरीत चिन्हो के अन्तः खण्ड काटती है ।
04:46View Solution