आधारभूत समानुपातिकता प्रमेय सिद्ध कीजिए प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य - बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है । ( याद कीजिए कि आप इसे IX में सिद्ध कर चुके हैं । )
Step by step video & image solution for आधारभूत समानुपातिकता प्रमेय सिद्ध कीजिए प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य - बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है । ( याद कीजिए कि आप इसे IX में सिद्ध कर चुके हैं । ) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.3
16 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.4
9 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - बहुविकल्पी प्रश्न
26 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - बहुविकल्पी प्रश्न
7 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - MBD HINDI-HARYANA BOARDCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - लघु उत्तरात्मक प्रश्न
21 Videos
Similar Questions
बताई कि आकृति में दिए त्रिभुजों के युग्मों में से कौन - कौन से युग्म समरूप हैं । उस समरूपता की कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए ।
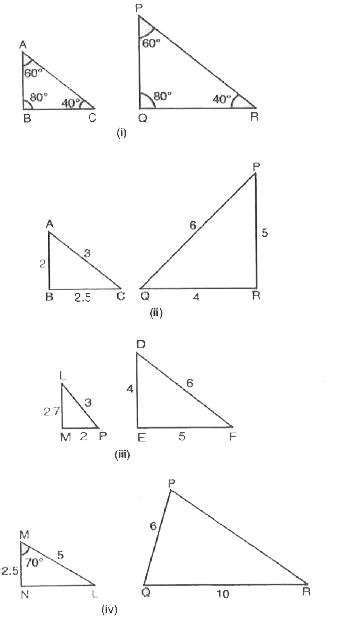
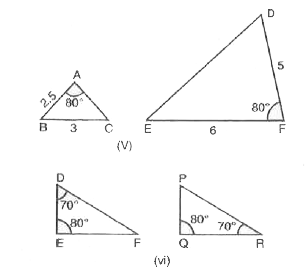
View Solutionमान लीजिए ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64cm2 और 121cm2 हैं । यदि EF = 15.4 cm हो , तो BC ज्ञात कीजिए ।
View SolutionΔABC और ΔDEF में ∠A=40∘,∠B=80∘,∠C=60∘,∠D=60∘,∠E=80∘,∠F=40∘ हो तो
View Solutionपहाड़ी के शिखर से उसके पाद के 40 किमी दूरी का अवनमन कोण 45∘ है । पहाड़ी की ऊँचाई होगी :
( A ) 30 किमी ( B ) 35 किमी
( C ) 40 किमी ( D ) 45 किमी ।
View Solutionनिम्न रैखिक समीकरण के युग्म को हल कीजिए ।
2x+3y=13
5x−4y=−2
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए (2+λ)x+(1+λ)y=5+7λ द्वारा निरूपित रेखायें λ के भिन्न-भिन्न मानों के लिए एक बिंदु से होकर जाती है। वह बिंदु ज्ञात कीजिए।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionनिर्देशाक्षो को प्रारंभिक निर्देशांकों के समांतर रखते हुए मूल बिंदु को बिंदु P पर हटाने पर समीकरण ax+by+c=0 समीकरण ax+by+c+λ=0 के रूप में बदल जाता है सिद्ध कीजिए कि P बिन्दुपथ ax+by=λ होगा ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionकिसी ΔOAB में ∠AOB=90∘ तथा बिन्दु P, Q भुजा AB को समत्रिभाजित करते हैं | सिद्ध कीजिए कि, OP2+OQ2=59AB2.
View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solution
