In a monthly unit test, the marks scored by Bunny and Sunny are in the ratio of and those scored by Bharat and Sunny are in the ratio of . If Bharat 112 marks, then find the marks scored by Bunny.
170
190
200
180
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Define the Variables
Let the marks scored by Bunny be B, the marks scored by Sunny be S, and the marks scored by Bharat be R.
Step 2: Set Up Ratios
From the problem, we know:
1. The ratio of marks scored by Bunny and Sunny is 10:7.
BS=107
This can be rewritten as:
B=107S(1)
2. The ratio of marks scored by Bharat and Sunny is 8:9.
RS=89
This can be rewritten as:
R=89S(2)
Step 3: Substitute the Known Value
We know that Bharat scored R=112 marks. Using equation (2):
112=89S
Step 4: Solve for S
To find S, we can rearrange the equation:
S=112×98
Calculating this gives:
S=112×1.125=126
Step 5: Substitute S Back to Find B
Now that we have S=126, we can substitute this value back into equation (1) to find B:
B=107×126
Calculating this gives:
B=10×18=180
Final Answer
Thus, the marks scored by Bunny are 180.
---
Let the marks scored by Bunny be B, the marks scored by Sunny be S, and the marks scored by Bharat be R.
From the problem, we know:
1. The ratio of marks scored by Bunny and Sunny is 10:7.
BS=107
This can be rewritten as:
B=107S(1)
RS=89
This can be rewritten as:
R=89S(2)
We know that Bharat scored R=112 marks. Using equation (2):
112=89S
To find S, we can rearrange the equation:
S=112×98
Calculating this gives:
S=112×1.125=126
Now that we have S=126, we can substitute this value back into equation (1) to find B:
B=107×126
Calculating this gives:
B=10×18=180
Thus, the marks scored by Bunny are 180.
Topper's Solved these Questions
- RATIO, PROPORTION AND VARIATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - Leval 2
20 Videos
- RATIO, PROPORTION AND VARIATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - Leval 3
10 Videos
- RATIO, PROPORTION AND VARIATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - Essay Type Questions
5 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONSEXERCISE - Level 3
23 Videos
- SALES TAX AND COST OF LIVING INDEX BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SALES TAX AND COST OF LIVING INDEX EXERCISE - Level 3
14 Videos
Similar Questions
Marks scored by 100 students in a 25 marks unit test of Mathematics is given below. Their median is
View SolutionThe line chart given below shows the marks scored by 2 students P and Q in five subjects.
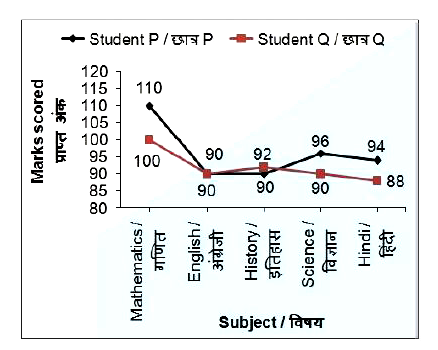
What is the ratio of the marks scored by student P in Science to the marks scored by student Q in History?
View Solution
Knowledge Check
In a test, A scored 10% more than Band B scored 5% more then C.If C scored 300 marks out of 400,then A's marks are
A310B325C350D360To qualify an examination of 200 marks, a candidate should obtain 40% marks. If A scores 10% more than the passing marks, then what is the marks obtained by A?
A80B78C88D68
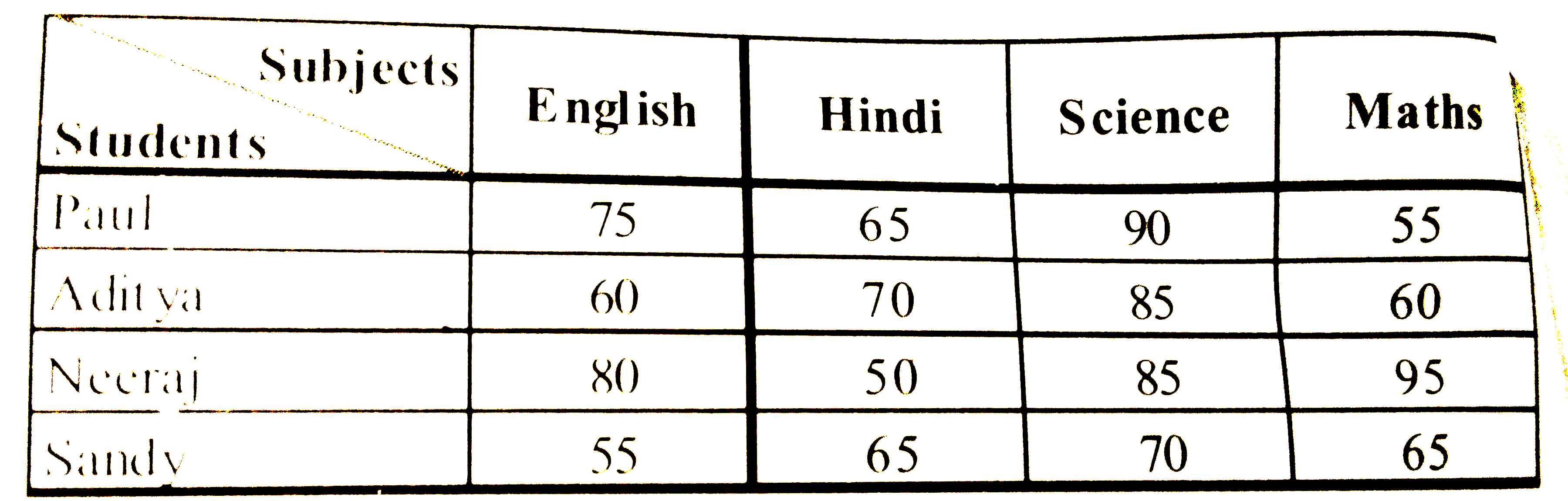
Find the average of the marks scored by Aditya in English, Hindi and Science together ?
View Solution
Find the ratio of total marks scored by all four students together in Hindi to total marks scored by all foud students together in in Science ?
View SolutionVicky scored x marks in Maths and Rakesh scored x3 marks in Maths. The proudct of their marks was 256. Find their marks.
View SolutionShantan got 68 marks in English and 85 marks in Mathematics. Find the ratio of the marks scored in English to the Matematics.
View SolutionThe marks scored ina test by a class of 25 boys are as folowing
View SolutionThe ratio of marks obtained by Amal, Bimal and Komal in an examination is 12:8:15. Find the marks obtained by Bimal and Komal, if Amal scored 15 marks less than that of Komal.
View Solution
