In the adjoining figure, AXB is an arc of the circle. C and D are the points on the remaining part of the circle.

Angle made by an arc in the same sagment are equal.
∴∠ADB=∠ACB
⇒∠ADB=30∘.
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question
25 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 31
9 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
In the following figure, AB is an arc of the circle, C and D are the points on the circle. If ∠ACB=30∘, Find ∠ADB.

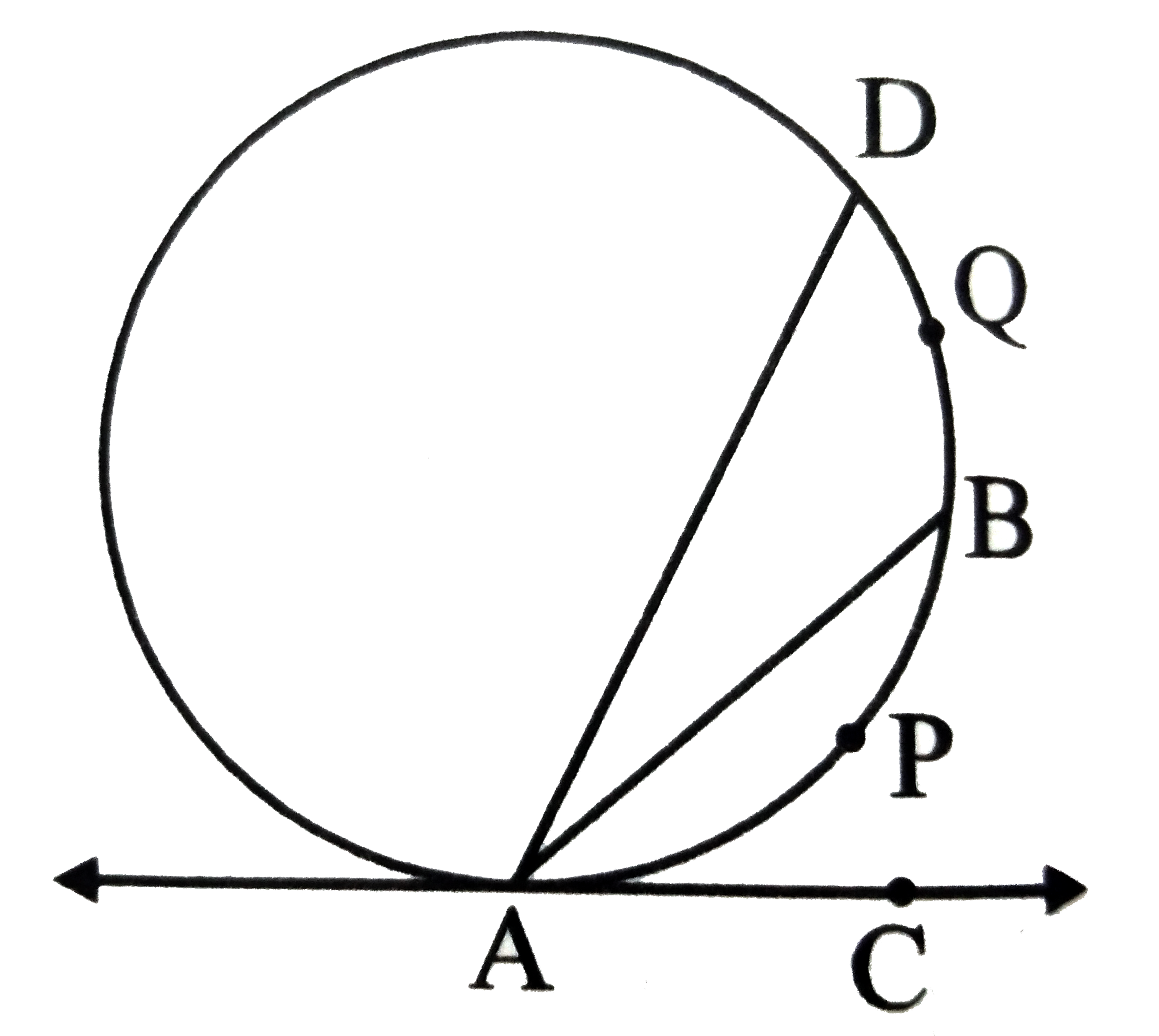
View SolutionIn the adjoining figure, seg AB and seg AD are chords of the circle . C is a point on tangent to the circle at point A. IF m(arc APB)=80∘and ∠BAD=30∘, then find
(i) ∠BAC (ii) m(arc BQD)
View Solution
Knowledge Check
In the adjoining figure ABC is an equilateral triangle and C is the centre of the circle, A and B lie on the circle. What is the area of the shaded region , if the diameter of the circle is 28 cm ?
 A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the above
A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the aboveIn the adjoining figure, O is the centre of the circle and D ∠OBD=50∘. Find the ∠BAD :
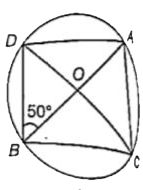 A60∘B40∘C80∘D45∘
A60∘B40∘C80∘D45∘
In the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
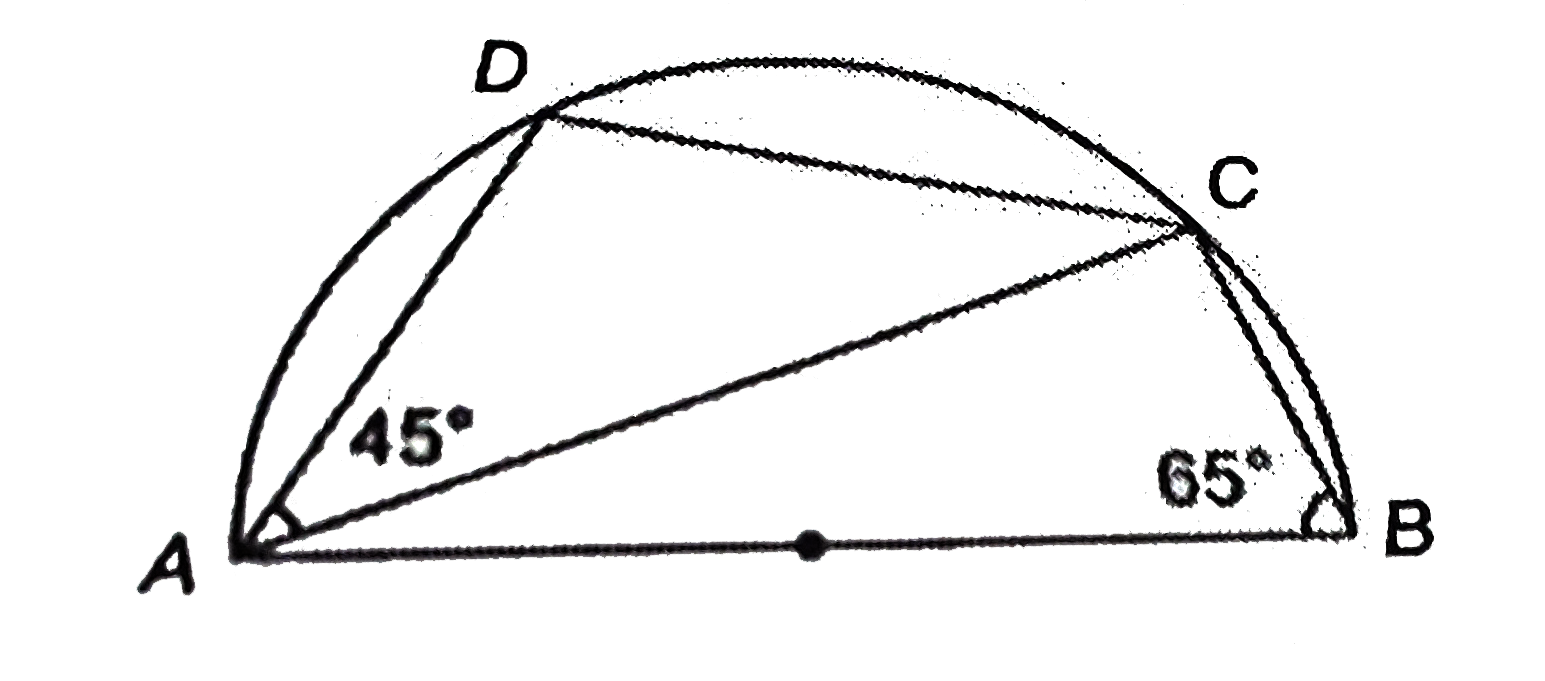
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.

View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure, AB is a diameter of the circle, C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).

View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
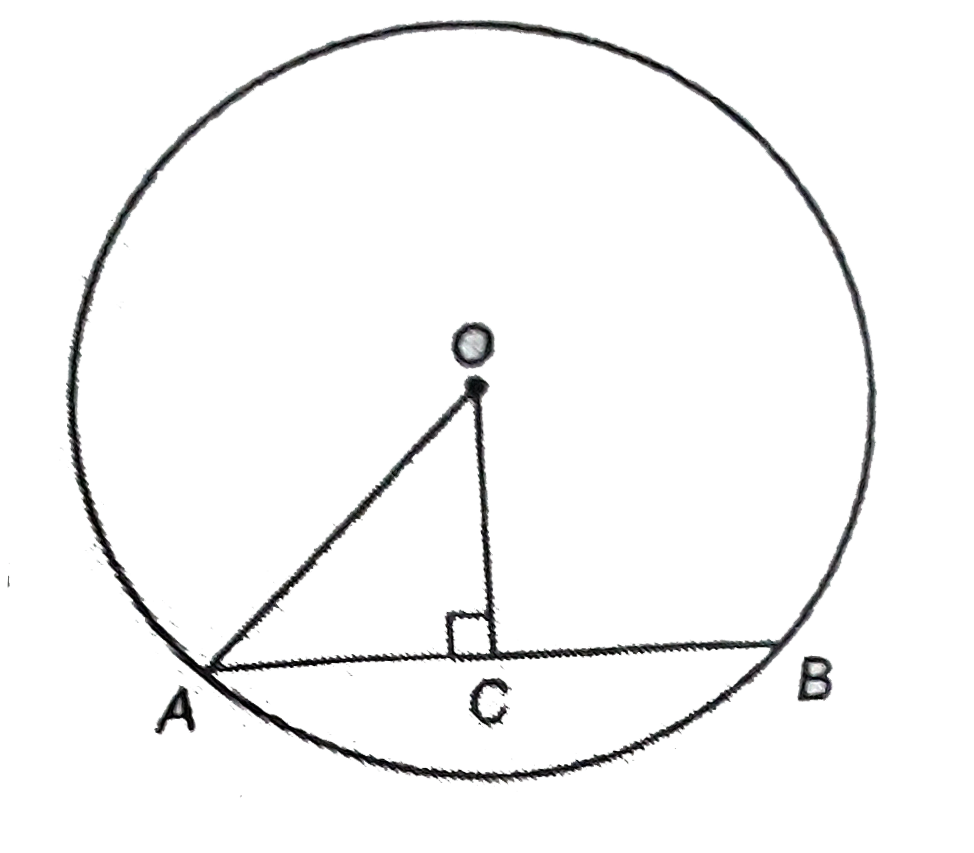
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
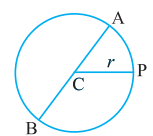
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
View Solution
