Draw the Vennn diagrems to illustrate the following relationship among the sets E,M and U , where E is the set of students studying English in a school , M is the set of students studying Mathematics in the same scholl , U is the set of all students in that school .
(i) All the students who study Mathematics study English , but some students who study English do not study Matchematics .
(ii) There is not students who studies both Mathematics and English.
(iii) Some of the students study Mathematics but do not study English , some study English but do not study Mathematics , and some study both .
(iv) Not all students study Matchematics , but every student studyin English studies Mathematics.
To illustrate the relationships among the sets E (students studying English), M (students studying Mathematics), and U (all students in the school) using Venn diagrams, we will follow these steps for each condition given in the question.
1. Draw the Universal Set (U): Start by drawing a rectangle to represent the universal set U, which contains all students in the school.
2. Draw Set M (Mathematics): Inside the rectangle, draw a circle for set M. This circle represents all students studying Mathematics.
3. Draw Set E (English): Draw another circle for set E that completely encompasses set M. This indicates that all students studying Mathematics are also studying English.
4. Indicate Students Studying Only English: Leave a portion of circle E outside of circle M to show that some students study English but not Mathematics.
(ii) There are no students who study both Mathematics and English.
1. Draw the Universal Set (U): Start with the rectangle for the universal set U.
2. Draw Set M (Mathematics): Draw a circle for set M.
3. Draw Set E (English): Draw another circle for set E, ensuring that the two circles do not overlap at all. This indicates that there are no students who study both subjects.
(iii) Some students study Mathematics but do not study English, some study English but do not study Mathematics, and some study both.
1. Draw the Universal Set (U): Start with the rectangle for the universal set U.
2. Draw Set M (Mathematics): Draw a circle for set M.
3. Draw Set E (English): Draw another circle for set E, ensuring that the two circles overlap. This overlap represents students who study both subjects.
4. Indicate Students Studying Only Mathematics: Leave a portion of circle M outside of circle E.
5. Indicate Students Studying Only English: Leave a portion of circle E outside of circle M.
(iv) Not all students study Mathematics, but every student studying English studies Mathematics.
1. Draw the Universal Set (U): Start with the rectangle for the universal set U.
2. Draw Set M (Mathematics): Draw a circle for set M, ensuring it does not encompass the entire rectangle.
3. Draw Set E (English): Draw another circle for set E that is entirely within circle M. This indicates that every student studying English also studies Mathematics.
4. Indicate Students Not Studying Mathematics: Leave a portion of the rectangle outside of circle M to show that not all students study Mathematics.
2. Draw Set M (Mathematics): Inside the rectangle, draw a circle for set M. This circle represents all students studying Mathematics.
3. Draw Set E (English): Draw another circle for set E that completely encompasses set M. This indicates that all students studying Mathematics are also studying English.
4. Indicate Students Studying Only English: Leave a portion of circle E outside of circle M to show that some students study English but not Mathematics.
2. Draw Set M (Mathematics): Draw a circle for set M.
3. Draw Set E (English): Draw another circle for set E, ensuring that the two circles do not overlap at all. This indicates that there are no students who study both subjects.
2. Draw Set M (Mathematics): Draw a circle for set M.
3. Draw Set E (English): Draw another circle for set E, ensuring that the two circles overlap. This overlap represents students who study both subjects.
4. Indicate Students Studying Only Mathematics: Leave a portion of circle M outside of circle E.
5. Indicate Students Studying Only English: Leave a portion of circle E outside of circle M.
2. Draw Set M (Mathematics): Draw a circle for set M, ensuring it does not encompass the entire rectangle.
3. Draw Set E (English): Draw another circle for set E that is entirely within circle M. This indicates that every student studying English also studies Mathematics.
4. Indicate Students Not Studying Mathematics: Leave a portion of the rectangle outside of circle M to show that not all students study Mathematics.
Topper's Solved these Questions
- SETS BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - Frequently Asked Questions
26 Videos
- SETS BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - EXERCISE 1 (a) (Short Answer Type Questions)
7 Videos
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - CHAPTER TEST
12 Videos
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Chapter Test
7 Videos
Similar Questions
150 students are studying English, Maths or both. 62 per cent of the students are studying English and 68 per cent are studying Maths. How many students are studying both?
View SolutionEach student in a class of 40, studies at least one of the subjects English, Mathematics and Economics.16 study English, 22 Economics and 26 Mathematics, 5 study English and Economic, 14 Mathematics and Economics and 2 study all the three subjects. The number of students who study English and Mathematics but not Economics is
View Solution
Knowledge Check
Study the following table carefully and answer the questions given below :
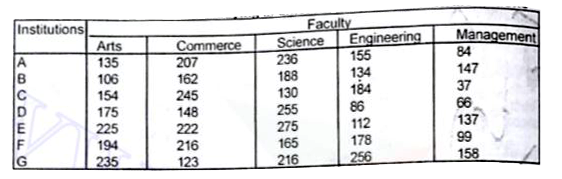
What is the percentage of students studying Management with respect to the total number of students studying in the institute B ?A10%B20%C30%D5%The number of students enrolled in different faculties in a school is as follows

The percentage of students studying in Science and Vocational Subject is:A1. 37.2B2. 23C3. 25D4. 9.3In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry , 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
A30B20C10DNone of These
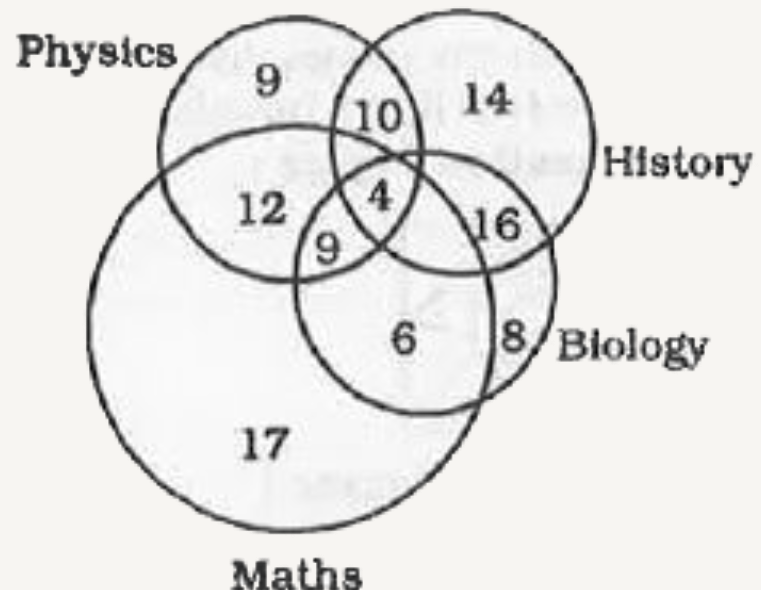
The diagram represents the number of students studying different subjects. What is the number of students who study History and Biology?
View SolutionIn a class of 50 students, each student passed Maths or English. If 10 students passed both Maths and English, and 30 students passed Maths, the find the number of students who passed English.
View SolutionIn a class of 50 students, each student passed Maths or English. If 10 students passed both Maths and English, and 30 students passed Maths, the find the number of students who passed English.
View SolutionWhat is the ratio of the number of students studying science of colleges A and B together to the number of students studying commerce incolleges D and E together?
View SolutionIn class XI of a school,40% of the students study Mathematics and 30% study Biology. If a student is selected at random from the class, then find the probability that he will be studying Mathematics or Biology
View Solution
