In the following , state whether A=B or not :
(i) A = {a,b,c,d}, B= {d,c,b,a}
(ii) A= {4,8,12,16},B= {8,4,16,18}.
(iii) A={2,4,6,8,10},
B=x:x is a positive even integer and x≤10}
(iv) A= {x:x is multiple of 10},
B= {10,15,20,25,30,.....}.
The correct Answer is:(i) A=B
(ii) A≠B
(iii) A=B
(iv) A≠B.
To determine whether the sets A and B are equal, we need to check if they contain the same elements. Two sets are considered equal if they have exactly the same elements, regardless of the order in which they are listed.
Let's analyze each part step by step:
Part (i)
- Given Sets:
- A = {a, b, c, d}
- B = {d, c, b, a}
Step 1: Count the elements in both sets.
- Set A has 4 elements: a, b, c, d.
- Set B has 4 elements: d, c, b, a.
Step 2: Check if the elements are the same.
- Both sets contain the same elements: a, b, c, d.
Conclusion: Since both sets have the same elements, A = B.
Part (ii)
- Given Sets:
- A = {4, 8, 12, 16}
- B = {8, 4, 16, 18}
Step 1: Count the elements in both sets.
- Set A has 4 elements: 4, 8, 12, 16.
- Set B has 4 elements: 8, 4, 16, 18.
Step 2: Check if the elements are the same.
- Set A contains 12, which is not in Set B.
- Set B contains 18, which is not in Set A.
Conclusion: Since the elements are not the same, A ≠ B.
Part (iii)
- Given Sets:
- A = {2, 4, 6, 8, 10}
- B = {x : x is a positive even integer and x ≤ 10}
Step 1: Identify the elements of Set B.
- The positive even integers less than or equal to 10 are: 2, 4, 6, 8, 10.
Step 2: Compare the elements of both sets.
- Set A = {2, 4, 6, 8, 10}
- Set B = {2, 4, 6, 8, 10}
Conclusion: Since both sets have the same elements, A = B.
Part (iv)
- Given Sets:
- A = {x : x is a multiple of 10}
- B = {10, 15, 20, 25, 30, ...}
Step 1: Identify the elements of Set A.
- Set A includes all multiples of 10: 10, 20, 30, 40, ...
Step 2: Compare the elements of both sets.
- Set A includes: 10, 20, 30, 40, ...
- Set B includes: 10, 15, 20, 25, 30, ...
Step 3: Check for common elements.
- Set B contains 15 and 25, which are not multiples of 10.
Conclusion: Since the elements are not the same, A ≠ B.
Final Summary:
- (i) A = B
- (ii) A ≠ B
- (iii) A = B
- (iv) A ≠ B
- Given Sets:
- A = {a, b, c, d}
- B = {d, c, b, a}
- Set A has 4 elements: a, b, c, d.
- Set B has 4 elements: d, c, b, a.
- Both sets contain the same elements: a, b, c, d.
- Given Sets:
- A = {4, 8, 12, 16}
- B = {8, 4, 16, 18}
- Set A has 4 elements: 4, 8, 12, 16.
- Set B has 4 elements: 8, 4, 16, 18.
- Set A contains 12, which is not in Set B.
- Set B contains 18, which is not in Set A.
- Given Sets:
- A = {2, 4, 6, 8, 10}
- B = {x : x is a positive even integer and x ≤ 10}
- The positive even integers less than or equal to 10 are: 2, 4, 6, 8, 10.
- Set A = {2, 4, 6, 8, 10}
- Set B = {2, 4, 6, 8, 10}
- Given Sets:
- A = {x : x is a multiple of 10}
- B = {10, 15, 20, 25, 30, ...}
- Set A includes all multiples of 10: 10, 20, 30, 40, ...
- Set A includes: 10, 20, 30, 40, ...
- Set B includes: 10, 15, 20, 25, 30, ...
- Set B contains 15 and 25, which are not multiples of 10.
- (i) A = B
- (ii) A ≠ B
- (iii) A = B
- (iv) A ≠ B
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - NCERT- FILE QUESTION FROM NCERT BOOK (EXERCISE 1.3)9videos
SETS
- BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - NCERT- FILE QUESTION FROM NCERT BOOK (EXERCISE 1.4)12videos
SETS
- BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - NCERT- FILE QUESTION FROM NCERT BOOK (EXERCISE 1.1)5videos
SETS
- BOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - CHAPTER TEST12videos
SEQUENCES AND SERIES
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Chapter Test7videos
STATISTICS
Similar Questions
In the following, state whether A = B or not :
(i) A={a,b,c,d}
(ii) B={d,c,b,a}
(iii) A={2,4,6,8,10}
B = {x : x is positive even integer and x≤10}
(iv) A = {x : x is a multiple of 10}
B={10,15,20,25,30,...}.View SolutionIn the following, state whether A=Bor not:(i) A={a,b,c,d} B={d,c,b,a}(ii) A={4,8,12,16} B={8,4,16,18}(iii) A={2,4,6,8,10} B = {x: x is po
View SolutionFrom the following pairs, write whether A = B or not :
(i) A={2,4,8,12},B={8,4,2,12}
(ii) A={3,4},B={x:x is a root of x2−7x+12=0}
(iii) A={x:x is a multiple of 10},B={10,15,20,25,30,....}
(iv) A={x:x is a letter of the word 'FOLLOW'},B={x:x is a letter of the word 'WOLF'}
(v) A={x:2x2−5x+2=0},B={x:2x3−5x2+2x=0}
(vi) A={x:x∈N,1≤x≤3},B={x:3x=9,2x=2,x−1=1}.View SolutionIn each of the following cases, state whether A=B or A≠B.
(i)A={a,b,c,d,e}B={x:x is first five letters of English alphabet}
(ii)A'{0},B={x:x is a natural number less than 1}
(iii)A={1,5,25,125},B={x:x is a positive divisor of 125}
(iv)A={x:x is a multiple of 10} B={10,15,20,25,30,....}View SolutionLet A ={3,6,12,15,18,21} and B- {4,8,12,16,20} and C = {2,4,6,8,10,12,14,16} , then :
(i) A-B = ………
(ii) B-C = ……..View SolutionIn which of the following tables a and b vary inversely:
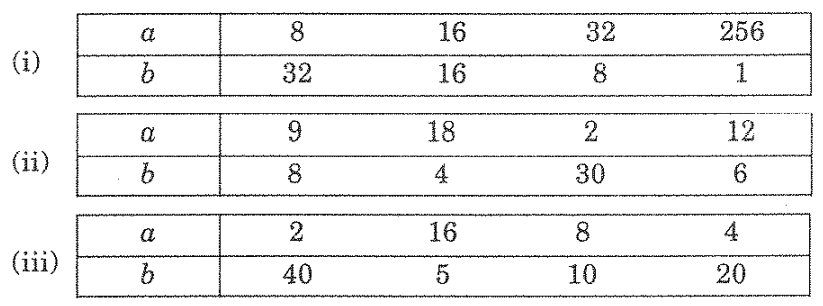 View Solution
View SolutionWhich of the following are co-primes? 8, 10 (b) 9, 10 (c) 6, 8 (d) 15, 18
View SolutionWrite the following sets in Set - Builder Form :
(a) (i) A={0}
(ii) B={-1,1}
(iii) C={1,3,5,7,9}
(iv) D={2,4,6,8}
(v) E={1,5,10,15,……}
(vi) F= {12,18,24,…,96}.
(b) (i) ,6,9,12}
(iii) {2,4,8,16,32}
(iii) {5,25,125,625}
(iv) {2,4,6,....}
(v) {1,4,9,.....100}View SolutionLet A={3,6,12,15,18,21}, B={4,8,12,16,20}, C={2,4,6,8,10,12,14,16}and D={5,10,15,20} . Find: B−D
View SolutionLet A={3,6,12,15,18,21}, B={4,8,12,16,20}, C={2,4,6,8,10,12,14,16}and D={5,10,15,20} . Find: B−C
View Solution

