If A = {1,2} and B= {a,b,c}, obtain A×B and represent it by an arrow diagram
To solve the problem of finding the Cartesian product A×B where A={1,2} and B={a,b,c}, we will follow these steps:
1. Understanding Cartesian Product:
The Cartesian product A×B consists of all possible ordered pairs (m,n) where m is an element from set A and n is an element from set B.
2. Listing Elements of Set A and Set B:
- Set A contains the elements: 1,2
- Set B contains the elements: a,b,c
3. Forming Ordered Pairs:
We will pair each element of A with every element of B:
- For the first element of A (which is 1):
- Pair with a: (1,a)
- Pair with b: (1,b)
- Pair with c: (1,c)
- For the second element of A (which is 2):
- Pair with a: (2,a)
- Pair with b: (2,b)
- Pair with c: (2,c)
4. Combining All Ordered Pairs:
Now, we combine all the ordered pairs we formed:
A×B={(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
5. Representing with an Arrow Diagram:
- Draw two circles: one for set A and one for set B.
- In the circle for set A, write the elements 1 and 2.
- In the circle for set B, write the elements a,b,c.
- Draw arrows from each element in set A to each element in set B:
- From 1 to a, b, and c.
- From 2 to a, b, and c.
Final Answer:
The Cartesian product A×B is:
A×B={(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
The Cartesian product A×B consists of all possible ordered pairs (m,n) where m is an element from set A and n is an element from set B.
- Set A contains the elements: 1,2
- Set B contains the elements: a,b,c
We will pair each element of A with every element of B:
- For the first element of A (which is 1):
- Pair with a: (1,a)
- Pair with b: (1,b)
- Pair with c: (1,c)
- For the second element of A (which is 2):
- Pair with a: (2,a)
- Pair with b: (2,b)
- Pair with c: (2,c)
Now, we combine all the ordered pairs we formed:
A×B={(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
- Draw two circles: one for set A and one for set B.
- In the circle for set A, write the elements 1 and 2.
- In the circle for set B, write the elements a,b,c.
- Draw arrows from each element in set A to each element in set B:
- From 1 to a, b, and c.
- From 2 to a, b, and c.
The Cartesian product A×B is:
A×B={(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Frequently Asked Questions
17 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Illustrative Example
54 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CHAPTER TEST
12 Videos
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
Knowledge Check
Diagram A and B represents?
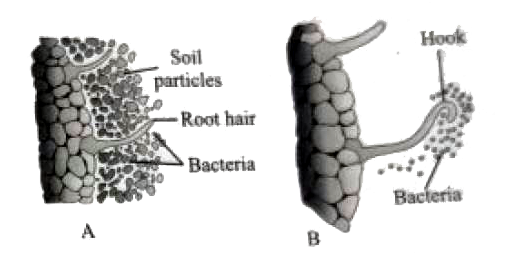 AA-Bacteria get modified into rod-shaped bacteroidsBB-Successful infection of root hairCB-Successful infection of root hairDB-Bacterial division occurs
AA-Bacteria get modified into rod-shaped bacteroidsBB-Successful infection of root hairCB-Successful infection of root hairDB-Bacterial division occursIf A={1,2},B={2,3}andC={3,4} then find A×(B∩C).
A{(2,3),(4,3)}B{(1,3),(2,3)}C{(2,2),(2,3)}D{(1,4),(2,4)}
If A=(a,b,c) and B=(1,2,3) then find A×B.
View SolutionIf A={2,4,6,8} and B={1,3,5,7} then represent A×B graphically.
View SolutionIf A={a,b,c} and B={1,2,3} then write the A×B and B×A what do you notice ? Represent them in three diagram.
View SolutionIf A={1,3,5},B={x,y} find the following products A×B (ii) B×A (iii) A×A (iv) B×B
View SolutionIf A={1,2,4}and B={1,2,3} , represent following sets - B×B
View SolutionIf A={1,2,4}and B={1,2,3} , represent following sets - A×B
View Solution
