For the relation y=+√x, say whether it is a function or not. If it is a function, find its domain and range.
To determine whether the relation y=+√x is a function, and if so, to find its domain and range, we can follow these steps:
Step 1: Determine if it is a function
A relation is a function if for every input x in the domain, there is exactly one output y. In the case of y=+√x:
- For any non-negative value of x (i.e., x≥0), there is one corresponding value of y.
- For example:
- If x=0, then y=+√0=0.
- If x=1, then y=+√1=1.
- If x=4, then y=+√4=2.
Since each input x gives exactly one output y, we conclude that y=+√x is indeed a function.
Step 2: Find the domain
The domain of a function is the set of all possible input values (i.e., x values) for which the function is defined.
- The expression √x is defined only for non-negative values of x.
- Therefore, the domain of y=+√x is:
Domain=(0,∞)
Step 3: Find the range
The range of a function is the set of all possible output values (i.e., y values) that the function can produce.
- Since y=+√x produces non-negative outputs for all x in the domain:
- When x=0, y=0.
- As x increases, y also increases without bound.
Thus, the range of y=+√x is:
Range=(0,∞)
Final Conclusion
The relation y=+√x is a function with:
- Domain: (0,∞)
- Range: (0,∞)
---
A relation is a function if for every input x in the domain, there is exactly one output y. In the case of y=+√x:
- For example:
- If x=0, then y=+√0=0.
- If x=1, then y=+√1=1.
- If x=4, then y=+√4=2.
Since each input x gives exactly one output y, we conclude that y=+√x is indeed a function.
The domain of a function is the set of all possible input values (i.e., x values) for which the function is defined.
- Therefore, the domain of y=+√x is:
Domain=(0,∞)
The range of a function is the set of all possible output values (i.e., y values) that the function can produce.
- When x=0, y=0.
- As x increases, y also increases without bound.
Thus, the range of y=+√x is:
Range=(0,∞)
The relation y=+√x is a function with:
- Domain: (0,∞)
- Range: (0,∞)
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise-2(a)
25 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 2(b)
14 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Frequently Asked Questions
17 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CHAPTER TEST
12 Videos
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
In the given function, find the co-domain and range
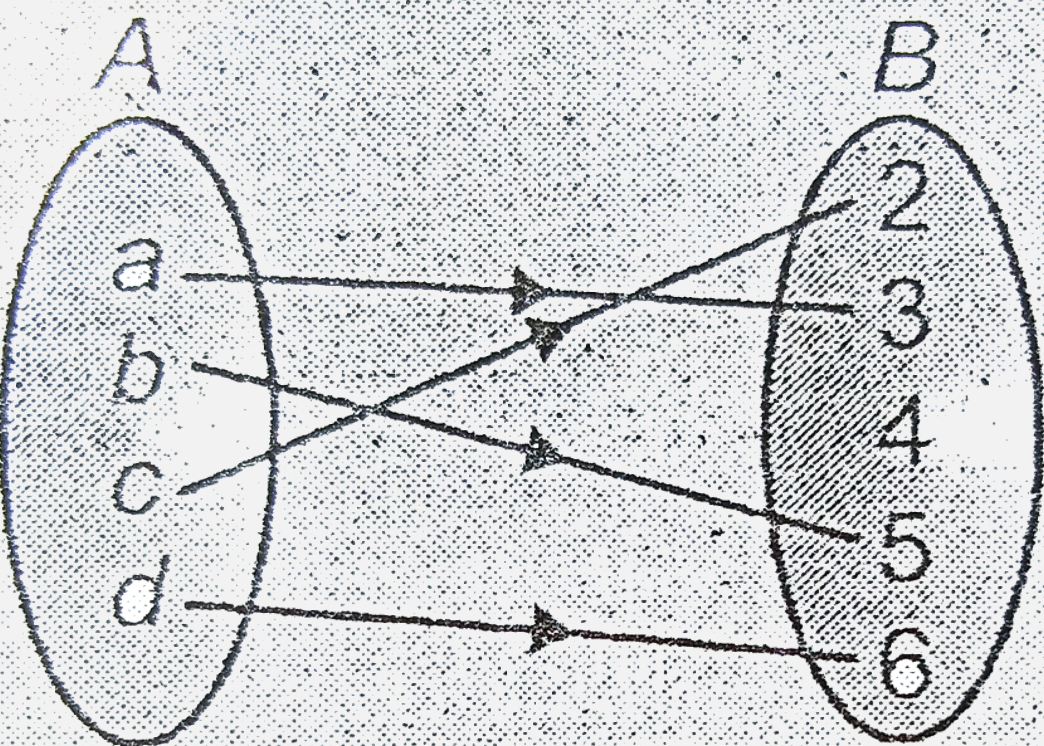
View SolutionIn the given function, find the domain, co-domain and range.
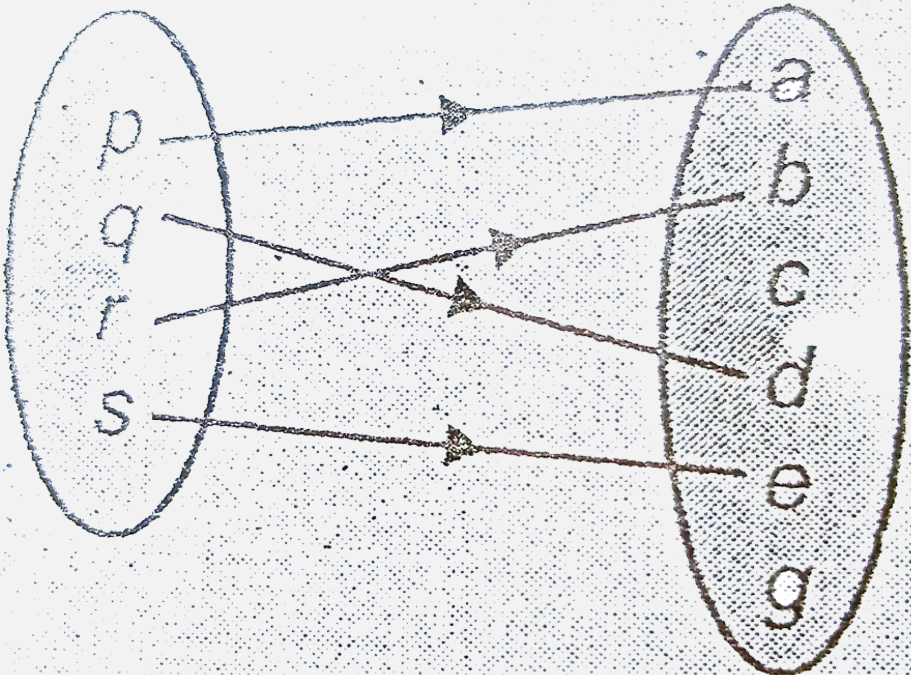
View SolutionDefinition OF relation and function domain and range
View SolutionDomain and Range of a function
View SolutionIntroduction to function | Odd even function | Domain range
View SolutionWrite the domain and range of the signum function,
View SolutionRelation between domain and function of composite functions
View SolutionLet R be a relation defined on the set of natural numbers as:
R={(x,y):y=3x,y∈N}
Is R a function from N to N? If yes find its domain, co-domain and range.
View SolutionRange and domain of a functions

View SolutionFind the domain of the function y=sinx
View Solution
