If any two rows (or columns) of a determinant are identical, the value of the determinant is zero.
To prove that if any two rows (or columns) of a determinant are identical, then the value of the determinant is zero, we can follow these steps:
1. Define the Determinant:
Let's consider a 3x3 determinant A as follows:
A=∣∣
∣∣a11a12a13a21a22a23a31a32a33∣∣
∣∣
For our proof, we will assume that the first two rows are identical:
A=∣∣
∣∣a11a12a13a11a12a13a31a32a33∣∣
∣∣
Hint: Start by defining a determinant with identical rows or columns.
2. Apply Row Operations:
We can perform a row operation on the determinant. Specifically, we can replace the first row with the result of subtracting the second row from the first row:
R1→R1−R2
This gives us:
A=∣∣
∣∣000a11a12a13a31a32a33∣∣
∣∣
Hint: Use row operations to simplify the determinant.
3. Evaluate the Determinant:
The determinant now has an entire row of zeros (the first row). The property of determinants states that if any row (or column) of a determinant is all zeros, then the value of the determinant is zero:
A=0
Hint: Remember that a determinant with a row or column of zeros equals zero.
4. Generalize the Result:
The above argument can be applied similarly if we assume two identical columns instead of rows. Thus, if any two rows or columns of a determinant are identical, the value of the determinant is always zero.
Hint: The proof holds for both rows and columns, reinforcing the generality of the statement.
Conclusion:
We have shown that if any two rows (or columns) of a determinant are identical, the value of the determinant is zero. This completes the proof.
Let's consider a 3x3 determinant A as follows:
A=∣∣
∣∣a11a12a13a21a22a23a31a32a33∣∣
∣∣
For our proof, we will assume that the first two rows are identical:
A=∣∣
∣∣a11a12a13a11a12a13a31a32a33∣∣
∣∣
We can perform a row operation on the determinant. Specifically, we can replace the first row with the result of subtracting the second row from the first row:
R1→R1−R2
This gives us:
A=∣∣
∣∣000a11a12a13a31a32a33∣∣
∣∣
The determinant now has an entire row of zeros (the first row). The property of determinants states that if any row (or column) of a determinant is all zeros, then the value of the determinant is zero:
A=0
The above argument can be applied similarly if we assume two identical columns instead of rows. Thus, if any two rows or columns of a determinant are identical, the value of the determinant is always zero.
We have shown that if any two rows (or columns) of a determinant are identical, the value of the determinant is zero. This completes the proof.
Topper's Solved these Questions
- DETERMINANTSBOOK - MODERN PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - OBJECTIVE TYPE QUESTIONS (Very short answer type question)
26 Videos
- DETERMINANTSBOOK - MODERN PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - NCERT FILE (Exercise 4.1)
13 Videos
- DETERMINANTSBOOK - MODERN PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - OBJECTIVE TYPE QUESTIONS (Fill in the blanks)
10 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - MODERN PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - CHAPTER TEST
12 Videos
- DIFFERENTIAL EQUATIONSBOOK - MODERN PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - CHAPTER TEST (9)
12 Videos
Similar Questions
Knowledge Check
If any two adjacent rows or columns of a determinant are intercharged in position, the value of the determinant :
ABecomes zeroBRemains the sameCChanges its signDIs doubledIf any two adjacent rows or columns of a determinant are interchanged in position, the value of the determinant
AA. Becomes zeroBB. Remains the sameCC. Changes its signDD. Is doubledIn figure, determine the value of y.
 A25∘B35∘C15∘D40∘
A25∘B35∘C15∘D40∘
Two rows(or columns) are identical or proportional the value of the determinant is
View SolutionIf any two rows(columns) of a square matrix A=[aij] of order (n≥2) are identical, then its determinant is 0.
View SolutionIn the figure ,find the value of x.

View SolutionIn Figure, determine the value of y.
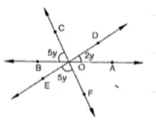
View SolutionIn figure, determine the value of y.
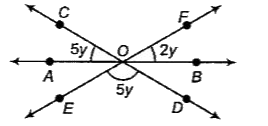
View Solution
